Solving the Platform and Object Kinetic Energy Equation

[eyespy]

Homework Statement

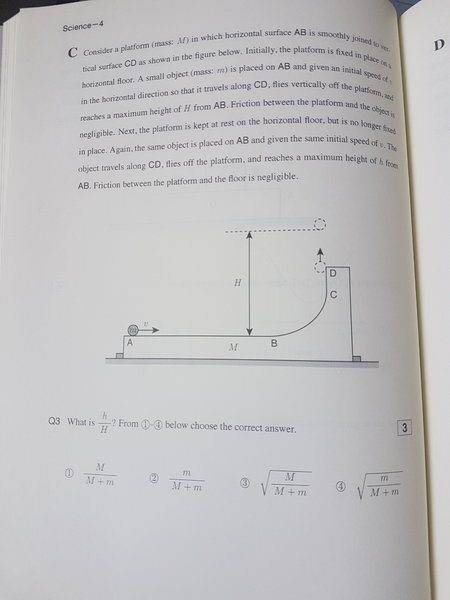
Consider a platform (mass: M) which horizontal surface AB s smoothly joined to vertical surface CD as shown in the figure below. Initially, the platform is fixed in place on a horizontal floor. A small object (mass: m) is placed on AB and given an initial speed of v in the horizontal direction so that it travels along CD, flies vertically off the platform, and reaches a maximum height of H from AB. Friction between the platform and the object is negligible. Next, the platform is kept at rest on the horizontal floor, but is no longer fixed in place. Again, the same object is placed on AB and given the same initial speed of v. The object travels along CD, floes off platform, and reaches a maximum height of from AB. Friction between the platform and the floor is negligible.

Relevant Equations

K1 + U1 = K2 + U2

Homework Statement:: Consider a platform (mass: M) which horizontal surface AB s smoothly joined to vertical surface CD as shown in the figure below. Initially, the platform is fixed in place on a horizontal floor. A small object (mass: m) is placed on AB and given an initial speed of v in the horizontal direction so that it travels along CD, flies vertically off the platform, and reaches a maximum height of H from AB. Friction between the platform and the object is negligible. Next, the platform is kept at rest on the horizontal floor, but is no longer fixed in place. Again, the same object is placed on AB and given the same initial speed of v. The object travels along CD, floes off platform, and reaches a maximum height of from AB. Friction between the platform and the floor is negligible.
Homework Equations:: K1 + U1 = K2 + U2

I found H being him: (v²)/2g, using the Ek1 + U1 = Ek2 + U2 --> Ek1 = U2.
The problem was finding the "h".
I tried for many hours, and failed. So I tried to see the answer and resolving it backwards to find out where the source came from. And then I came to the conclusion that the kinetic energy of the platform equals the potential energy of the platform plus the potential energy of the small object.

You can see this with this:
h/(v²/2g) = M/(M+m) ---> h = (Mv²)/2g*(M+m) = EkM/g*(M+m) --> EkM = hg(M+m) = UM + Um.
The question is, how did he come to the conclusion that the kinetic energy of the platform equals its potential energy plus the potential energy of the ball?

 

[PeroK]

Homework Statement:: Consider a platform (mass: M) which horizontal surface AB s smoothly joined to vertical surface CD as shown in the figure below. Initially, the platform is fixed in place on a horizontal floor. A small object (mass: m) is placed on AB and given an initial speed of v in the horizontal direction so that it travels along CD, flies vertically off the platform, and reaches a maximum height of H from AB. Friction between the platform and the object is negligible. Next, the platform is kept at rest on the horizontal floor, but is no longer fixed in place. Again, the same object is placed on AB and given the same initial speed of v. The object travels along CD, floes off platform, and reaches a maximum height of from AB. Friction between the platform and the floor is negligible.
Homework Equations:: K1 + U1 = K2 + U2

Homework Statement:: Consider a platform (mass: M) which horizontal surface AB s smoothly joined to vertical surface CD as shown in the figure below. Initially, the platform is fixed in place on a horizontal floor. A small object (mass: m) is placed on AB and given an initial speed of v in the horizontal direction so that it travels along CD, flies vertically off the platform, and reaches a maximum height of H from AB. Friction between the platform and the object is negligible. Next, the platform is kept at rest on the horizontal floor, but is no longer fixed in place. Again, the same object is placed on AB and given the same initial speed of v. The object travels along CD, floes off platform, and reaches a maximum height of from AB. Friction between the platform and the floor is negligible.
Homework Equations:: K1 + U1 = K2 + U2

View attachment 253851

I found H being him: (v²)/2g, using the Ek1 + U1 = Ek2 + U2 --> Ek1 = U2.
The problem was finding the "h".
I tried for many hours, and failed. So I tried to see the answer and resolving it backwards to find out where the source came from. And then I came to the conclusion that the kinetic energy of the platform equals the potential energy of the platform plus the potential energy of the small object.

You can see this with this:
h/(v²/2g) = M/(M+m) ---> h = (Mv²)/2g*(M+m) = EkM/g*(M+m) --> EkM = hg(M+m) = UM + Um.
The question is, how did he come to the conclusion that the kinetic energy of the platform equals its potential energy plus the potential energy of the ball?

I don't understand that solution. The platform has no change in potential energy.

In the second case, to calculate $H$, you should use conservation of momentum in the horizontal direction.

 

[eyespy]

I don't understand that solution. The platform has no change in potential energy.

In the second case, to calculate $H$, you should use conservation of momentum in the horizontal direction.

Me too, but in feedback the answer is: (M / (m + M)). So h/H = (M/(m+M))

 

[PeroK]

Me too, but in feedback the answer is: (M / (m + M)). So h/H = (M/(m+M))

That's the answer. But, how do you get that answer using conservation of x-momentum and conservation of energy?

Note: The final answer is a simple function of $m, M$. If you solve a completely different problem using $m$ and $M$ - a gravitational problem, say - then you might get the same answer $M/(m+M)$. That might be why you can get the same answer by looking at the "potential of $M$".

 

[eyespy]

That's the answer. But, how do you get that answer using conservation of x-momentum and conservation of energy?

Note: The final answer is a simple function of $m, M$. If you solve a completely different problem using $m$ and $M$ - a gravitational problem, say - then you might get the same answer $M/(m+M)$. That might be why you can get the same answer by looking at the "potential of $M$".

Honestly I do not know. To find out the height in the first situation I simply used energy conservation, as it can reach a certain height was easy. The problem was in the second case, I did not understand how the fact that the platform is free can change the height. Does the platform move along with the sphere?
To find "H" I used: (mv²)/2 = mgH --> H = v²/2g. So from this I deduced that it would have something to do with energy to find the height "h"

 

[PeroK]

Honestly I do not know. To find out the height in the first situation I simply used energy conservation, as it can reach a certain height was easy. The problem was in the second case, I did not understand how the fact that the platform is free can change the height. Does the platform move along with the sphere?
To find "H" I used: (mv²)/2 = mgH --> H = v²/2g. So from this I deduced that it would have something to do with energy to find the height "h"

Yes, the platform moves and takes some of the energy. Hence we expect $h < H$.

What about conservation momentum in the x-direction?

 

[eyespy]

Yes, the platform moves and takes some of the energy. Hence we expect $H < h$.

What about conservation momentum in the x-direction?

If the platform consumes part of the energy of the ball, why is it higher in the second case?

Sorry, I don't know how to calculate the horizontal energy conservation. I found this exercise at EJU (Examination for Japanese University Admission for International Students). I'm going to the 3rd grade of high school. If possible I would like you to explain to me how to calculate this horizontal energy conservation, can be any other example. I'm not an American, so it's a little hard to watch English videos.

 

[PeroK]

If the platform consumes part of the energy of the ball, why is it higher in the second case?

Sorry, I don't know how to calculate the horizontal energy conservation. I found this exercise at EJU (Examination for Japanese University Admission for International Students). I'm going to the 3rd grade of high school. If possible I would like you to explain to me how to calculate this horizontal energy conservation, can be any other example. I'm not an American, so it's a little hard to watch English videos.

I got $h$ and $H$ mixed up. It's lower in the second case. I'm just going offline now!

It's a tricky problem. But, if you don't know about conservation of momentum then you should learn about that.

 

[eyespy]

I got $h$ and $H$ mixed up. It's lower in the second case. I'm just going offline now!

It's a tricky problem. But, if you don't know about conservation of momentum then you should learn about that.

Thanks, I think tha I got the direction :)