Two negatively charged balloons on strings. Find tensions?

  • Thread starter Thread starter cvang24
  • Start date Start date
  • Tags Tags
    Charged Strings
Click For Summary
SUMMARY

The discussion centers on analyzing the tension in the strings of two negatively charged balloons that are in equilibrium. The balloons, which have unequal charges (Q > q) and unequal masses (M > m), require a free body diagram to identify the forces acting on each balloon. The conclusion drawn is that the tension in the string of the heavier balloon (T1) is greater than that in the lighter balloon (T2) due to the balance of gravitational and electrostatic forces.

PREREQUISITES
  • Understanding of electrostatic forces and charges
  • Knowledge of free body diagrams and equilibrium conditions
  • Familiarity with Newton's laws of motion
  • Basic principles of tension in strings
NEXT STEPS
  • Study the principles of electrostatics and Coulomb's law
  • Learn how to construct and analyze free body diagrams
  • Explore Newton's laws of motion in detail
  • Investigate the concept of equilibrium in physics
USEFUL FOR

Students studying physics, particularly those focusing on electrostatics and mechanics, as well as educators looking for examples of tension analysis in equilibrium problems.

cvang24
Messages
1
Reaction score
0

Homework Statement



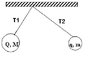
"Two balloons are rubbed with wool. Let us assume that the two balloons are at
rest (in equilibrium), have unequal charges (Q > q) and
unequal masses (M > m).

In which string is the tension greater, T1 or T2?
Show your work for your conclusion.
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    16 KB · Views: 497
Physics news on Phys.org
Hi cvang, welcome to PF.
According to the rules of the Forums, you have to show your attempt for solution.
Start with free body diagram. What forces act on each balloon?

ehild
 

Similar threads

Why are the forces on torque tension and not the weight of the mass?
  • · Replies 7 ·
Replies
7
Views
2K
What is the Charge on Each Balloon?
  • · Replies 3 ·
Replies
3
Views
2K
Finding Charge & Tension of a Suspended Cork Ball
  • · Replies 3 ·
Replies
3
Views
4K
Three equal charges held by equal length strings
  • · Replies 11 ·
Replies
11
Views
2K
Tension Force between two rotating masses on strings
  • · Replies 1 ·
Replies
1
Views
3K
Finding the pressure of a gas in three identical balloons
  • · Replies 12 ·
Replies
12
Views
2K
Find the tension in the lower string and the rotation rate
  • · Replies 9 ·
Replies
9
Views
5K
Calculating tensions and acceleration
  • · Replies 10 ·
Replies
10
Views
3K
How Does Zero Gravity Affect the Tension in Strings of Charged Bodies?
  • · Replies 3 ·
Replies
3
Views
1K
"Tension: T1 vs T2 - What is Correct?
  • · Replies 1 ·
Replies
1
Views
2K