budd99
- 5
- 0
Homework Statement
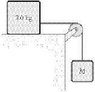
The system shown (attached image) is released from rest and moves 50 cm in 1.0 s. What is the value of M? All surfaces are frictionless.
a. 0.42 kg
b. 0.34 kg
c. 0.50 kg
d. 0.59 kg
e. 0.68 kg
Homework Equations
Since the incline is 90 degress, I am trying to model this as an Atwood machine.
I don't understand how there can be any acceleration if the mass that we need to find is smaller than 3kg.
The Attempt at a Solution
moves 50cm in 1s., which means a is 0.5m/s2
So, using the formula
a = (m2 -m1)/(m1 + m2)g
0.5 = (m2 - 3)(3 + m2)9.80
m2 = 3.32
Which is not in the solution