- #1
alpha358
- 9
- 0
Consider two parallel streams of electrons in vacuum. Each stream moves with constant velocity and carries a current. According to classical electrodynamics parallel and same direction currents attract each other.
The problem is that I can't see how relativistic length contraction can cause attraction in this situation.
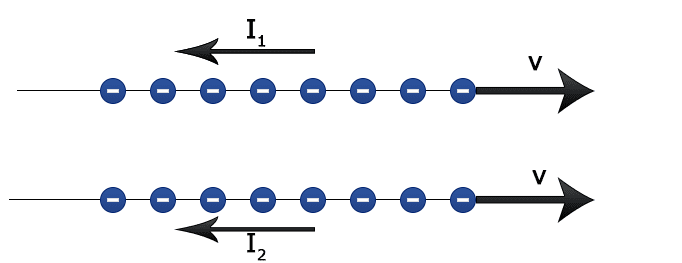
The problem is that I can't see how relativistic length contraction can cause attraction in this situation.
Attachments
Last edited: