Two rods, each with a free and a fixed ball and a spring

[Like Tony Stark]

Homework Statement

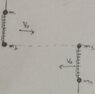
The picture shows two rods of negligible mass and length $d_0$. Both of them have a ball of mass $m$ in each end and a spring of natural length $d_0$ and constant $k$.
One of the balls of each rod is fixed, and the other one is freely to move along the rod.
Initially, the rods move with zero angular velocity.
At time $t=t_0$, the fixed balls of each rod collide inelastically.
1) Explain using words and equations what happens after the collision.
2) Determine the final angular velocity of the system
3) Determine the maximum compression of the spring
4) write the equation of motion for one of the balls after the collision
Neglect gravity.

Relevant Equations

$dL/dt=0$
$L=I\omega$

Since there are no external forces, the angular momentum ($L$) and linear momentum ($P$) are conserved.
Let's call the left rod $A$ and the right one $B$.
If all the balls were fixed, I'd write
$L_0=L_f$
$L_A+L_B=(I_A+I_B)\omega_f$
From this equation I can find the final angular velocity.
The rods "would form a larger single body" which rotates with $\omega_f$ and zero translation (because the velocity of the centre of mass is zero).
The equation of any ball would be
$n) T=mr\omega^2$
Where $T$ is the tension force and $r$ the distance between the mass and the centre or mass.But I don't know what difference the free balls and the spring make, I think it is related to the moments of inertia of the rods, but they don't have to change since the angular velocity changes for angular momentum to be conserved; if they changed, I'd have to calculate the new moments of inertia and the final angular velocity (three unknowns, one equation).

 

[haruspex]

I assume the diagram is your own. Can we be confident it correctly represents the set up? It would not have been at all clear to me from the words.

If correct, it seems odd to ask for maximum spring compression instead of maximum extension.

The rods "would form a larger single body"

It doesn't say they stick together, merely that it is completely inelastic. You should take that as meaning maximum KE is lost, consistent with other laws.

what difference the free balls and the spring make

None immediately, but it asks about subsequent motion.

 

[etotheipi]

It doesn't say they stick together, merely that it is completely inelastic. You should take that as meaning maximum KE is lost, consistent with other laws.

Doesn't it just say inelastically, and not completely inelastically, which is to say that there is no constraint that the loss of kinetic energy is a maximum (the only requirement is that $T_2 < T_1$, but it is not specified by how much)?

 

[haruspex]

Doesn't it just say inelastically, and not completely inelastically, which is to say that there is no constraint that the loss of kinetic energy is a maximum (the only requirement is that $T_2 < T_2$, but it is not specified by how much)?

You are right
I always get confused about which of elastic/inelastic is taken to mean perfectly so when unqualified. However, if the collision is only partly inelastic there's not enough information for (3).

 

[Like Tony Stark]

I assume the diagram is your own. Can we be confident it correctly represents the set up? It would not have been at all clear to me from the words.

Actually, that's the diagram that comes with the exercise.

 

[haruspex]

Actually, that's the diagram that comes with the exercise.

Ok, thanks for clarifying.

 

[Like Tony Stark]

I always get confused about which of elastic/inelastic is taken to mean perfectly so when unqualified. However, if the collision is only partly inelastic there's not enough information for (3).

The collision is perfectly inelastic, that's why I thought that the two rods will form a larger one.Why would the springs compress?

 

[haruspex]

The collision is perfectly inelastic, that's why I thought that the two rods will form a larger one.Why would the springs compress?

It may well be that instantaneously the colliding masses acquire the same velocity, but there is no reason to suppose they remain together thereafter.
As I implied, I don't think the springs will compress at first. Rather, they will stretch as the rods rotate. Later on they may compress.

 

[Like Tony Stark]

It may well be that instantaneously the colliding masses acquire the same velocity, but there is no reason to suppose they remain together thereafter.

Ok, so using conservation of linear momentum I can find the final angular velocity and the velocity of the centre of mass of each rod, with this information I can find the equation of motion of any ball.
The rods will move with translation, and after the collision, they move with translation and rotation.
Also, as angular momentum is to be conserved, $L_{A_0}+L_{B_0}=L_{A_f}+L_{B_f}$
If I know the initial angular momentum of each rod, the final angular velocities, and I suppose that the final moments of inertia are equal, I can find it from the equation.
Would this be the correct reasoning?

 

[haruspex]

Ok, so using conservation of linear momentum I can find the final angular velocity and the velocity of the centre of mass of each rod, with this information I can find the equation of motion of any ball.
The rods will move with translation, and after the collision, they move with translation and rotation.
Also, as angular momentum is to be conserved, $L_{A_0}+L_{B_0}=L_{A_f}+L_{B_f}$
If I know the initial angular momentum of each rod, the final angular velocities, and I suppose that the final moments of inertia are equal, I can find it from the equation.
Would this be the correct reasoning?

Sounds good.