U-tube Mercury: Pressure and Height Calculations with Pumped Right Side

[completenoob]

Homework Statement

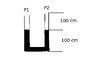
The u-tube shown has a cross-section of 1 cm^2. It contains mercury to the shown levels. The pressure above the the mercury is 750 torr. The left side is sealed off. The right side is is pumped such that the pressure is approximately zero.
i) Determine the far the mercury falls on the left side.
ii) Determine the pressure of the trapped air in the left side.
Temperature is constant

Homework Equations

$$P_1-P_2=\Delta h m g$$
$$m=\rho V$$

The Attempt at a Solution

i) If there is no air on the right hand side then 100cm of mercury has fallen.
ii)$$P_1=\Delta h m g$$ where $$\Delta h=200$$cm
Is this correct?

 

[LowlyPion]

$$P_1-P_2=\Delta h m g$$
$$m=\rho V$$

The Attempt at a Solution

i) If there is no air on the right hand side then 100cm of mercury has fallen.
ii)$$P_1=\Delta h m g$$ where $$\Delta h=200$$cm
Is this correct?

Consider the effect of the diminishing pressure on the sealed side as the column of mercury is drawn into the evacuated side.

 

[completenoob]

Well the pressure drop can be accounted for through $$\Delta P = \frac{nRT}{\Delta V}$$
This is all done at a constant T. I don't have a T!
but (i) is right, right?

 

[LowlyPion]

Well the pressure drop can be accounted for through $$\Delta P = \frac{nRT}{\Delta V}$$
This is all done at a constant T. I don't have a T!
but (i) is right, right?

No. Even if the one side remained open at 1 atm it would still only maintain 76cm of difference between 1 atm and the vacuum. (See mercury barometer.) As you reduce the pressure on the sealed side it will support less mercury in the column because it's pressure diminishes as it's sealed volume increases won't it?

http://www.uwsp.edu/geo/faculty/ritter/images/atmosphere/pressure_wind/merc_barometer.jpg

 

[completenoob]

So how should I go about it?

 

[LowlyPion]

Initially p = 1 atmosphere = 101325 Pascals = 760 mm Hg = 76.0 cm Hg
To make things simpler work in cm.

For any change in h between the levels of Hg between the 2 sides, you will have an h/2 increase in volume right?
So ...

100 V = (100 + h/2) V'
V = (100 + h/2)/100 V'

If p*v is constant (which it is if temp isn't changing) then that means that as the air is evacuated on 1 side and the level drops, the initial pressure must drop inversely to the way volume increases. So normally at 1 atm you have the relationship from Pascal that ...

ρ*g*h = P = 76.0 cm Hg

So you need to factor in then the effect of the increasing volume on the pressure to determine h

 

[completenoob]

Thank you for your help Lowly.
However my professor said that I should be solving a quadratic to find the height of the mercury; that does not seem right to me though. Yours makes more sense.

 

[completenoob]

Initially p = 1 atmosphere = 101325 Pascals = 760 mm Hg = 76.0 cm Hg
To make things simpler work in cm.

For any change in h between the levels of Hg between the 2 sides, you will have an h/2 increase in volume right?
So ...

100 V = (100 + h/2) V'
V = (100 + h/2)/100 V'

If p*v is constant (which it is if temp isn't changing) then that means that as the air is evacuated on 1 side and the level drops, the initial pressure must drop inversely to the way volume increases. So normally at 1 atm you have the relationship from Pascal that ...

ρ*g*h = P = 76.0 cm Hg

So you need to factor in then the effect of the increasing volume on the pressure to determine h

How did you get the h/2 increase in volume?
Could you explain the equation a little more? I don't get how you set it up exactly.

 

[completenoob]

anyone?

 

[completenoob]

Oh I see how you got the h/2.

So next we can say that: $$P_1 V_1 = P_2 V_2$$ which is $$P1 = P_2 \frac{V_2}{V_1}$$

And I think you meant $$P_1 = \rho g h A$$ at the top.

I let the height be a variable x of the mercury.

So $$V1 = \frac{2 x +h}{2 x} V_2$$. Plugging that into the top equation and rearranging I get:

$$h^2 \rho g A + 2 x \rho h g A - P_2 = 0$$

Is that right? And P2=0

 

[LowlyPion]

No need to introduce another variable x. You already have h.

Consider that if you have your P*V = P'*V' relationship, and that you want to compare that with the 1 atm case where you know that a vacuum supports 76 cm of Hg.

So as before if the volume of your sealed area is to change from 100 to 100 +h/2. (You can discard the idea of Area here because the volume is linearly proportional to length alone.)

If as before when I suggested:

V = (100 + h/2)/100 V'

Then P' = 100/(100 + h/2) P as the level drops.

Hence you can apply that to the notion that 76 = p*g*h at 1 atm such that you can say

P'/P = 100/(100 + h/2) = h/76 (keep in mind that pressure here can be measured in h of Hg.)

 

[completenoob]

huh..I'm sorry, I just don't see where your going with this in the end.

 

[completenoob]

Can anyone else assist me with this problem? I don't know why I don't see it.

 

[LowlyPion]

huh..I'm sorry, I just don't see where your going with this in the end.

Looks to me like there is 1 equation and 1 unknown - h.

Me ... I would solve for h.