RipClaw
- 11
- 0
Hi guys,
I find it quite difficult to visualize torque.
The picture I use as reference could be found here.
http://hyperphysics.phy-astr.gsu.edu/hbase/tord.html
I have had this disk with spindle thing & had tried rotating it.
But I did not feel anything in the direction of torque.(red arrow)
What is torque ?
Is it just a direction like North & South ?
When I open & close a door, what goes up & what comes down ?
[Other things like angular-velocity could be easily observed, say, for eg, marking dots at different radii on the disc]
I will be glad if somebody can ignite me to think in the right direction, by explaining it in layman's terms.
(Equations & derivations are available everywhere)
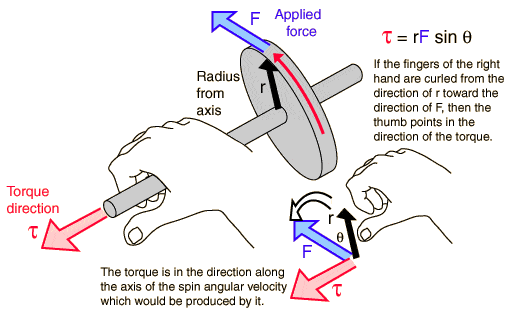
I find it quite difficult to visualize torque.
The picture I use as reference could be found here.
http://hyperphysics.phy-astr.gsu.edu/hbase/tord.html
I have had this disk with spindle thing & had tried rotating it.
But I did not feel anything in the direction of torque.(red arrow)
What is torque ?
Is it just a direction like North & South ?
When I open & close a door, what goes up & what comes down ?
[Other things like angular-velocity could be easily observed, say, for eg, marking dots at different radii on the disc]
I will be glad if somebody can ignite me to think in the right direction, by explaining it in layman's terms.
(Equations & derivations are available everywhere)
