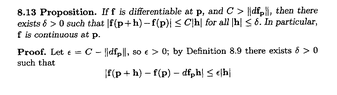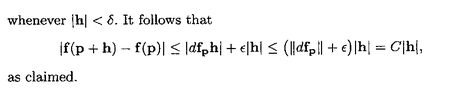MHB Understand Andrew Browder's Prop 8.13: Math Analysis Introduction

[Math Amateur]

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 8: Differentiable Maps and am specifically focused on Section 8.2 Differentials ... ...

I need some further help in fully understanding the proof of Proposition 8.13 ...

Proposition 8.13 reads as follows:
View attachment 9404
View attachment 9405
I think that a fully detailed proof of Proposition 8.13 reads somewhat as follows:Browder's Definition 8.9 essentially means that $$\text{df}_p$$ exists if $$ \lim_{ h \to 0 } \frac{1}{| h | } (f(p + h) - f(p) - \text{df}_p h ) = 0$$
Thus ... if we take $$\epsilon = C - \| df_p \|$$ then we can find $$\delta$$ such that ...$$| | h | \lt \delta \Longrightarrow \frac{1}{ | h | } | (f(p + h) - f(p) - \text{df}_p h ) - 0 | \leq \epsilon$$ ... ... ... (1)so that $$| h | \lt \delta \Longrightarrow | (f(p + h) - f(p) - \text{df}_p h ) | \leq \epsilon | h | $$ ... ... ... (2)Now the reverse triangle inequality (Duistermaat & Kolk Lemma 1.1.7 (iv) ) states that$$\| x - y \| \geq | \ \| x \| - \| y \| \ |$$Using the reverse triangle inequality we have $$| (f(p + h) - f(p) ) - ( \text{df}_p h ) | \geq | \ | f(p + h) - f(p) | - | \text{df}_p h ) | \ | $$ ... ... ... (3)Now (2) and (3) $$\Longrightarrow $$$$| \ | f(p + h) - f(p) | - | \text{df}_p h ) | \ | \leq \epsilon |h|$$ $$\Longrightarrow | f(p + h) - f(p) | \leq | \text{df}_p h | + \epsilon |h|$$
Now $$| \text{df}_p h ) | \leq | \text{df}_p | | h ) |$$ (Is that correct? ) ... so that ...$$| f(p + h) - f(p) | \leq | \text{df}_p | | h ) | + \epsilon |h|$$
$$\Longrightarrow | f(p + h) - f(p) | \leq ( \| \text{df}_p \| + \epsilon ) |h| + C |h|$$
Is that correct?Now ... my specific problem is how to rigorously and validly make the move $$| \ | f(p + h) - f(p) | - | \text{df}_p h ) | \ | \leq \epsilon |h|$$ $$\Longrightarrow | f(p + h) - f(p) | \leq | \text{df}_p h | + \epsilon |h|$$... ... since I have effectively ignored the modulus signs around $$\ | f(p + h) - f(p) | - | \text{df}_p h ) |$$ ...
... that is I have assumed that $$| f(p + h) - f(p) | \geq | \text{df}_p h ) |$$ ...
Can someone please explain how i deal with this issue ...

Help will be much appreciated ...

Peter

 

[Opalg]

Now ... my specific problem is how to rigorously and validly make the move $$| \ | f(p + h) - f(p) | - | \text{df}_p h ) | \ | \leq \epsilon |h|$$ $$\Longrightarrow | f(p + h) - f(p) | \leq | \text{df}_p h | + \epsilon |h|$$... ... since I have effectively ignored the modulus signs around $$\ | f(p + h) - f(p) | - | \text{df}_p h ) |$$ ...
... that is I have assumed that $$| f(p + h) - f(p) | \geq | \text{df}_p h ) |$$ ...
Can someone please explain how i deal with this issue ...

For real numbers $X$ and $Y$, $|X|\leqslant Y$ means $-Y\leqslant X\leqslant Y$. In particular, $|X|\leqslant Y \Longrightarrow X\leqslant Y$.

In this case, $| f(p + h) - f(p) | - | \text{df}_p h | \leqslant\bigl| \ | f(p + h) - f(p) | - | \text{df}_p h | \bigr| \leqslant | \text{df}_p h ) |$.

 

[Math Amateur]

For real numbers $X$ and $Y$, $|X|\leqslant Y$ means $-Y\leqslant X\leqslant Y$. In particular, $|X|\leqslant Y \Longrightarrow X\leqslant Y$.

In this case, $| f(p + h) - f(p) | - | \text{df}_p h | \leqslant\bigl| \ | f(p + h) - f(p) | - | \text{df}_p h | \bigr| \leqslant | \text{df}_p h ) |$.

Thanks for a most helpful Post, Opalg

Peter