Rob D
Gold Member
- 15
- 0
Please forgive this most basic and fundamental of algebra questions but as I enter the calculus arena there is one small algebra function that has eluded intuitive understanding. In factoring quadratics and other polynomials, I am very successfully able to work the operations of factoring but one thing bugs me. I'm a self-educating 64 yo physics student so I have no teacher or colleague to ask.
Where did the middle term come from?
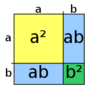
If I factor: 4x2 - 28x + 49 I get (2x-7)(2x-7) or (2x-7)2
If I then "FOIL" the terms (2x)(2x)-14x-14x +(-7x)(-7x) I again get 4x2-28x+49
Intuitively, at least for my old brain, (2x-7)2 gives 4x2+49
Just writing this down I'm feeling dumb but using this method how or why is the 28x generated from (2x-7)2?
Many thanks and Sorry for the High School question.
Where did the middle term come from?
If I factor: 4x2 - 28x + 49 I get (2x-7)(2x-7) or (2x-7)2
If I then "FOIL" the terms (2x)(2x)-14x-14x +(-7x)(-7x) I again get 4x2-28x+49
Intuitively, at least for my old brain, (2x-7)2 gives 4x2+49
Just writing this down I'm feeling dumb but using this method how or why is the 28x generated from (2x-7)2?
Many thanks and Sorry for the High School question.