Understanding Kirchhoff's Laws: Solving Circuits with Multiple Voltage Sources

[fluidistic]

Homework Statement

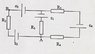
See picture for the problem.
1)Calculate the work done to move a charge a= 0.7 x 10 ^(-3)C from A to B, passing by R2.
2)The power dissipated in R3.
3)The current passing by R1.


2. Given equations
R1=R3=100 omhs, R2=200 ohms, R4=300 omhs.
e1=e3= 5 V, e2=10 V and e4=15 V.

The Attempt at a Solution

I realize that the problem is very simple if only I get the current passing through each branch of the circuit. However, applying Kirchhoff's law of voltage, I reach non sense.


More precisely, let i1 be the current passing through e3, let's suppose it in the clockwise direction. Let i3 be the current passing through the e1 branch, suppose its direction as down. Let i2 be the current passing through R3, anticlockwise.
Then I get, according to Kirchhoff's law of voltage:
\varepsilon _3 - \varepsilon _2 - \varepsilon _1 - i_1 R_2 -i_3 R_1=0 and \varepsilon _4 - i_2(R_3+R_4)- \varepsilon _1 - i_3R_1 =0.
From it I reach i_1= -20V+400 i_2. Of course units cannot match so there's at least an error. But I don't know where. I don't see it in the arithmetic so I guess I've used wrongly Kirchhoff's law, but I don't see it...
Thanks for any help.

 

[rl.bhat]

The equation becomes
200*i1 = -20V + 400*i2.

 

[fluidistic]

The equation becomes
200*i1 = -20V + 400*i2.

Ok thanks, I'm going to check it out right now. However assuming that you're right, I'm still stuck with the same problem. I have that a current is equal to a a constant times another current, plus a voltage. What am I misunderstanding? I mean a current should have at least one unit, and a current units one.
So I guess I made an error writing down Kirchhoff's law?

Edit: Ok, I reached the equation you provided, I forgot the 200 term in the last step.
But I'm still stuck, as stated above, in the same post. :)

 

[rl.bhat]

Consider i3 as (i1 + i2). The two equations become
-10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2) Solve these two equations to find i1 and i2.

 

[fluidistic]

Consider i3 as (i1 + i2). The two equations become
-10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2) Solve these two equations to find i1 and i2.

Ok I will do it. I'm just curious about what I found, that a current is worth something senseless. I'm surprised there is no error in this. So you really confirm there is no error?

 

[rl.bhat]

Ok I will do it. I'm just curious about what I found, that a current is worth something senseless. I'm surprised there is no error in this. So you really confirm there is no error?

I don't understand what you mean by senseless.

 

[fluidistic]

I don't understand what you mean by senseless.

Ok. I reached the following equation: i_1=2i_2-\frac{1V}{10}. Although I realize I've not reached the final answer for i_1, I do realize that the left side of the equation is measured in amperes and that the right side of the equation is something measured in amperes + something measured in volts. It doesn't make sense to me. Could you please explain to me why it is possible? Or I'm missing something obvious?

I thank you for all your help and time, sir. I'm willing to learn as much as possible.

 

[rl.bhat]

You can write 1V/10 as 1V/(10 ohm). In that case have you got any problem?
Any way how did you get
i1 = 2*i2 - 1V/10 ?

If you add the two equations
-10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2)
you get
2*i1 + 3*i2 = 0

 

[fluidistic]

You can write 1V/10 as 1V/(10 ohm). In that case have you got any problem?
Any way how did you get
i1 = 2*i2 - 1V/10 ?

Ah yes, you're right! I totally missed this part, I should have carried the units.
I reached this from

The equation becomes
200*i1 = -20V + 400*i2.

If you add the two equations
-10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2)
you get
2*i1 + 3*i2 = 0

I was about to do this .

Thanks a lot for all. If I have any further problem I'll let you know.

 

[fluidistic]

I still have some problems.

If you add the two equations
-10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2)
you get
2*i1 + 3*i2 = 0

Are you sure you didn't make any error? In my first post I reached
\varepsilon _3 - \varepsilon _2 - \varepsilon _1 - i_1 R_2 -i_3 R_1=0, and
\varepsilon _4 - i_2(R_3+R_4)- \varepsilon _1 - i_3R_1 =0.
When I plug the values, I get these 2 equations:
-100(i_1+i_2)-10-200i_1=0, and
10-100i_2-100(i_1+i_2)-300i_2=0, which differ from your equations.
Solving for i_1, I reached i_1=-\frac{5i_2}{4}.

While I had reached i_1=2i_2-\frac{1V}{10 \Omega}.
So I can solve for i_2. I get i_2=\frac{2}{65}A. And thus i_1=-\frac{1}{26}A. Did I do something wrong?

How did you get -10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2) ?

 

[rl.bhat]

How did you get -10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2) ?
Yes. You are right.
It should be
+10 + 200i1 + 100(i1 + i2) =0 ...(1)
-10 + 400i2 + 100(i1 + i2) = 0...(2) ?

 

[fluidistic]

How did you get -10 + 200i1 + 100(i1 + i2) =0 ...(1)
10 + 400i2 + 100(i1 + i2) = 0...(2) ?
Yes. You are right.
It should be
+10 + 200i1 + 100(i1 + i2) =0 ...(1)
-10 + 400i2 + 100(i1 + i2) = 0...(2) ?

We are still not in agreement. This problem is a headache!

 

[rl.bhat]

I am getting i1 = 3/70 A and i2 = 2/70 A.
I think there is a problem in your sign convention. Will you state your sign conventions for Ε and I*R.
You have taken i1 in the clockwise direction. You have traversing the loop in the direction of i1. You have taken I*R product negative assuming here is a drop of potential. you have taken E3 positive, where as you are crossing it from positive terminal to negative terminal. Is it not a drop in potential?

 

[fluidistic]

I am getting i1 = 3/70 A and i2 = 2/70 A.
I think there is a problem in your sign convention. Will you state your sign conventions for Ε and I*R.
You have taken i1 in the clockwise direction. You have traversing the loop in the direction of i1. You have taken I*R product negative assuming here is a drop of potential. you have taken E3 positive, where as you are crossing it from positive terminal to negative terminal. Is it not a drop in potential?

Right about the clockwise direction for i_1. I might be wrong of course, but as you said, I took \varepsilon _3 as a "climb of potential", i.e. not a drop. Should it be a drop of potential?
If so, then I should take \varepsilon _1 and \varepsilon _2 as a climb of potential instead of a drop of potential as I took.

 

[rl.bhat]

Right about the clockwise direction for i_1. I might be wrong of course, but as you said, I took \varepsilon _3 as a "climb of potential", i.e. not a drop. Should it be a drop of potential?
If so, then I should take \varepsilon _1 and \varepsilon _2 as a climb of potential instead of a drop of potential as I took.

According to the convention, current moves from positive terminal to negative terminal in the external circuit, and from negative terminal to positive terminal inside the cell. So we are assuming that +ve terminal is at the higher potential.
So if you cross the cell from +ve to -ve terminal then it is a fall in potential.

 

[fluidistic]

According to the convention, current moves from positive terminal to negative terminal in the external circuit, and from negative terminal to positive terminal inside the cell. So we are assuming that +ve terminal is at the higher potential.
So if you cross the cell from +ve to -ve terminal then it is a fall in potential.

Ok thank you for all. I have to restart the whole problem.

 

[fluidistic]

I get i_1=\frac{3}{70}A as you, but I get i_2=-\frac{1}{35}A which differs from your value. The most extraneous thing is that I got i_1 via i_2.
I have that i_1=\frac{1}{10}+2i_2.

Anyway, let's assume you are right.
To answer the first question, is the work done q(\varepsilon _2 - i_1 R_2)?

2)Is the power dissipated in R_3 worth i_2 ^2 R_3?

In my result of a negative current, does that mean that it is positive but in the other than assumed direction?

 

[rl.bhat]

i2 = 2/70 A = 1/35 A. I have not considered the sign of the current.
Other results are correct.
The negative sign indicates that the assumed direction of the current not correct.

 

[fluidistic]

i2 = 2/70 A = 1/35 A. I have not considered the sign of the current.
Other results are correct.
The negative sign indicates that the assumed direction of the current not correct.

Thank you very much for all, once again. Problem solved!