suv79
- 65
- 0
Homework Statement
how did they get this ?? it is like a potential divider, can anyone explain...
Homework Equations
The Attempt at a Solution
this is what i got[/B]
yes i know about node voltage, i want the node at V_cnh1995 said:Are you familiar with node voltage method?
Your second term is correct involving V2, and if you had been consistent you'd have a corresponding correct expression involving V1. The method you are using for this is called Superposition.this is what i got
You are a couple of steps away. Use cross multiplication in the denominator.suv79 said:
Using cross multiplication, you will be able to cancel out Z2+Z3 in the denominator with that in the numerator. Then take Z3 common from the numerators and you are done.suv79 said:
How will you write this term in the denominatorsuv79 said:View attachment 95455
i don't really understand the last step here
I think you are making it unnecessarily complicated. Just apply the cross multiplication rule to the denominator of each term separately. It is just one step and you'll be done.suv79 said:
Let the two terms be A and B.cnh1995 said:I think you are making it unnecessarily complicated. Just apply the cross multiplication rule to the denominator of each term separately. It is just one step and you'll be done.
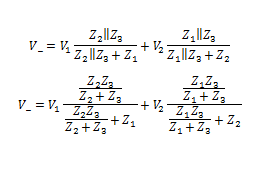

Um, that was my suggestion...suv79 said:yes please :)