SUMMARY
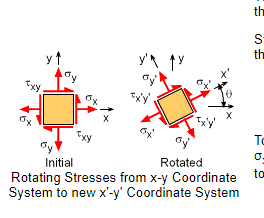
The discussion clarifies the concept of principal stress planes and their relationship to shear forces. When an element is rotated to a specific angle θ, it is indeed the principal stress plane where no shear force acts. The participants emphasize the importance of understanding transformations, particularly at 45-degree rotations, to transition between pure normal and pure shear stresses. The discussion highlights that complex stress cases can be understood through the superposition of simpler cases, reinforcing the foundational nature of these concepts in material mechanics.
PREREQUISITES
- Understanding of stress transformation in materials
- Familiarity with shear and normal stress concepts
- Knowledge of basic mechanics of materials
- Ability to interpret stress-strain relationships
NEXT STEPS
- Study the transformation of stress at 45-degree rotations
- Learn to derive the angle for pure shear from stress equations
- Explore the superposition principle in stress analysis
- Investigate differential surfaces and traction vectors in material mechanics
USEFUL FOR
Students and professionals in engineering, particularly those focused on material mechanics, structural analysis, and anyone seeking to deepen their understanding of stress transformations and shear forces.