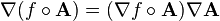Consider ##A = [a(x,y,z) \hat x + b(x,y,z) \hat y + c(x,y,z) \hat z ],## and ##f(A) = f(a,b,c),##
then ##\nabla f(A) = \hat x \frac{\partial f}{\partial x}\left[\frac{\partial a}{\partial x}+\frac{\partial b}{\partial x}+\frac{\partial c}{\partial x} \right] +
\hat y\frac{\partial f}{\partial y}\left[\frac{\partial a}{\partial y}+\frac{\partial b}{\partial y}+\frac{\partial c}{\partial y} \right]+
\hat z \frac{\partial f}{\partial z}\left[\frac{\partial a}{\partial z}+\frac{\partial b}{\partial z}+\frac{\partial c}{\partial z} \right]##
##\nabla f = \hat x \frac{\partial f}{\partial x}+ \hat y \frac{\partial f}{\partial y}+ \hat z \frac{\partial f}{\partial z}##
Also, ## \nabla A = \pmatrix{\frac{\partial a}{\partial x} &\frac{\partial b}{\partial x} & \frac{\partial c}{\partial x}\\
\frac{\partial a}{\partial y} &\frac{\partial b}{\partial y} & \frac{\partial c}{\partial y} \\
\frac{\partial a}{\partial z} &\frac{\partial b}{\partial z} & \frac{\partial c}{\partial z}}##
So if you carry out the matrix math and rearrange the terms,
You will see that the equation is true.