Undergrad Understanding the Definition of Cp and its Relationship to Cv: Explained

[11thHeaven]

Hi all, I'm working through a derivation of the general relationship between C_p and C_v and there's one point which is confusing me.

I understand that

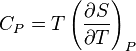
and

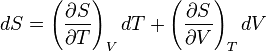
and that this implies the following:

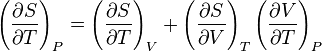
but isn't this equal to 0? Shouldn't the two partial derivatives on the right hand side, by the cyclic rule, multiply to -(∂S/∂T)_V?

I know that I'm missing something here but I can't work out what it is.

Help appreciated!

 

[Simon Bridge]

What you hold constant makes a difference.

 

[vanhees71]

Hm, I'm not sure what you want to derive, but let's start defining the heat capacities and see, where this leads to.

Start from energy conservation employing the 1st and 2nd fundamental laws
$$\mathrm{d} U=\mathrm{d} Q-p \mathrm{d} V=T \mathrm{d} S-p \mathrm{d} V.$$
This implies
$$C_V:=\left (\frac{\partial Q}{\partial T} \right)_{V}=\left (\frac{\partial U}{\partial T} \right)_V=T \left (\frac{\partial S}{\partial T} \right)_V.$$
For $C_p$ we need the enthalpy, given by the Legendre transform
$$H=U+p V ; \Rightarrow \; \mathrm{d} H=T \mathrm{d} S+V \mathrm{d} p,$$
and thus
$$C_p=\left (\frac{\partial H}{\partial T} \right )_p=T \left (\frac{\partial S}{\partial T} \right)_p.$$
Now we can use
$$\frac{C_p}{T}=\left (\frac{\partial S}{\partial T} \right)_p = \det \left (\frac{\partial(S,p)}{\partial(T,p)} \right) = \det \left (\frac{\partial(S,V)}{\partial(T,V)} \right) \det \left (\frac{\partial(T,V)}{\partial(T,p)} \right) = \left [ (\partial_T S)_V (\partial_V p)_T-(\partial_V S)_T (\partial_T p)_V \right ] (\partial_p V)_T = \frac{C_V}{T} - (\partial_p S)_T (\partial_T p)_V.$$
Now we can use the Gibb's free energy
$$G=U-TS+pV \; \Rightarrow \; \mathrm{d} G=-S \mathrm{d} T+V \mathrm{d} p,$$
to derive
$$\partial_p \partial_T G=-(\partial_p S)_T=\partial_T \partial_p G=(\partial_T V)_p$$
to get
$$C_p-C_v=T (\partial_T p)_V (\partial_T V)_p.$$