Cannot understand formula for molar heat capacities of an ideal gas

[vcsharp2003]

Homework Statement:: I am trying to understand a formula given in our book for determining molar heat capacity of an ideal gas under different thermodynamic processes using a single formula, but it is confusing. The exact formula for different processes is in the screenshots below. Can someone please explain how $x$ is calculated for different processes? The power of x is confusing me.
Relevant Equations:: As given in screenshot

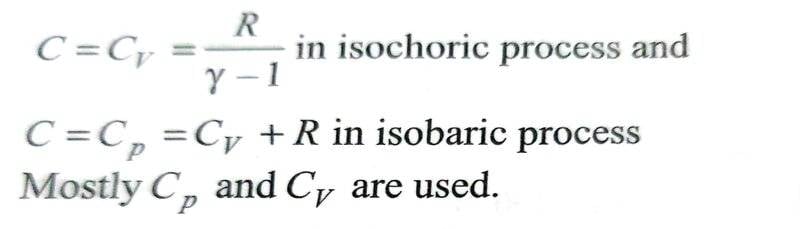
To apply the formula for molar heat capacity using the equation mentioned above, one needs to first determine $x$ value and plug it into the molar heat capacity formula. But I am hitting a roadblock in finding $x$ for certain processes like isochoric, isothermal and adiabatic processes. I do get it for isobaric process.

The equation $PV^x = constant$ doesn't make sense to me for isochoric process, in which $V$ is constant. To satisfy the above equation. $x$ would need to take a value so the left side of the equation is constant i.e. as $P$ increases, $V^x$ should decrease making $x$ take a variable set of multiple values. If, we can conclude that $x= \infty$ then the second term on right hand side will be $\frac {R}{1- \infty} = 0$, then the formula makes sense for isochoric process.

For isobaric process I get it. Since $P$ is already constant, so we need to only make sure that $V^x$ is constant, which is only true if $x=0$.

 

[Frabjous]

The generic ideal gas equation of state is PV=nRT. Assuming that the amount of gas does not change, you can write it as PV=kT. The isothermal, isobaric and isochroric EOS’s should be derived from in directly. Your book should have the adiabatic derivation of PV^ϒ=constant.

 

[vcsharp2003]

The generic ideal gas equation of state is PV=nRT. Assuming that the amount of gas does not change, you can write it as PV=kT. The isothermal, isobaric and isochroric EOS’s should be derived from in directly. Your book should have the adiabatic derivation of PV^ϒ=constant.

I get the adiabatic part that you mentioned which is based on derivation, but the book uses the value of x for other processes. I was hoping to know how the x value is reached.

 

[Frabjous]

My bad. The book says that it derives the equation later. Is that derivation consistent with V=constant?

 

[haruspex]

If $pV^x=constant$ for very large x then as p varies V hardly changes. In the limit, it doesn’t change at all.
I presume that just before the extract you show there was some other equation defining C. Would you post that please?

 

[Frabjous]

If $pV^x=constant$ for very large x then as p varies V hardly changes. In the limit, it doesn’t change at all.
I presume that just before the extract you show there was some other equation defining C. Would you post that please?

I assume that C is the molar heat capacity for a given process, $C = {\lim_{\Delta T \rightarrow 0}}{\frac {\Delta Q} {n \Delta T}}$. I am guessing that since there is no work involved in a constant volume process, the derivation assumes that there is some which is why the infinity appears.

 

[vcsharp2003]

If $pV^x=constant$ for very large x then as p varies V hardly changes. In the limit, it doesn’t change at all.
I presume that just before the extract you show there was some other equation defining C. Would you post that please?

Below are screenshots of full page from where the original post screenshots were extracted.

Screenshot 1

Screenshot 2

 

[vcsharp2003]

My bad. The book says that it derives the equation later. Is that derivation consistent with V=constant?

I think for adiabatic process of ideal gas we know that $PV^{\gamma} = constant$ is always true ( we don't care about the derivation of this equation for now since the goal is determining $x$ for different thermodynamic processes). Then we compare above equation with $PV^{x} = constant$ and we get $x= \gamma$. So, I am now also clear how $x$ is obtained for an adiabatic process.

 

[Frabjous]

I think for adiabatic process we know that for an ideal gas $PV^{gamma} = constant$. Then we compare above equation with $PV^{x} = constant$ and we get $x= \gamma$. So, I am now also clear how $x$ is obtained for an adiabatic process. My problem is only that I want to know how $x$ value is arrived at.

For a constant volume process, $\Delta Q = \Delta U$. I believe that when you look at the derivation of the equation, you will see that they using $\Delta Q = \Delta U + W$. The infinity is essentially showing up to drive W to zero. They say “we will derive it later“ on page 208 after the boxed C equation.

 

[Frabjous]

If $pV^x=constant$ for very large x then as p varies V hardly changes. In the limit, it doesn’t change at all.

Think about what @haruspex is saying here. It is not the common way we think about infinities in an equation.
You can write (P+δP)(V+δV)^x=constant. Since the limit of δV is zero, the only way it can influence the equation is if the limit of x is infinity and you get some zero-infinity action.

 

[vcsharp2003]

If $pV^x=constant$ for very large x then as p varies V hardly changes. In the limit, it doesn’t change at all.
I presume that just before the extract you show there was some other equation defining C. Would you post that please?

I think the following may be an apt way of getting the value of $x$ in an isochoric process.

We need to satisfy the equation $PV^{x} = constant$ when volume $V$ remains constant. We know for an isochoric process, the pressure $P$ must change and the only way $PV^{x} = constant$ is if $V^x =0$ else if we take finite value of $x$ then $V^x$ will be some constant number causing $PV^{x}$ to not remain constant as $P$ varies . Thus $V^x= 0 \implies x=-\infty$.

Now if we plug in $x=-\infty$ into the equation $C = \frac {R}{\gamma -1}. + \frac {R}{1 -x}$ then we get the second term on right hand side as $\frac {R}{1 - (-\infty)} = \frac {R}{\infty} = 0$. That gets us the correct formula for C in isochoric process using the framework mentioned in my original post. We get $C = \frac {R}{\gamma -1} + 0$ when volume $V$ is held constant.

 

[Chestermiller]

If you rewrite $PV^x=C$ as $$P^{\frac{1}{x}}V=C^{'}$$you can easily see how $x=\infty$ gives constant V.

 

[vcsharp2003]

If you rewrite $PV^x=C$ as $$P^{\frac{1}{x}}V=C^{'}$$you can easily see how $x=\infty$ gives constant V.

But then we will get in the left hand side $C^{\frac {1}{x}}$, which will not be a constant.

 

[Frabjous]

@Chestermiller
Is this formula for C used in practice (i.e., several other values of x that we care about)?

 

[Chestermiller]

But then we will get in the left hand side $C^{\frac {1}{x}}$, which will not be a constant.

The actual equation should read $$PV^x=P_0V_0^x$$What then?

 

[Chestermiller]

@Chestermiller
Is this formula for C used in practice (i.e., several other values of x that we care about)?

No. In my judgment, polytropic processes are used for pedagogical purposes only. In addition, I am strongly opposed to expressing heat capacity (which is supposed to be a function of state) in terms of Q (which is a function of path). lr is very confusing to students.

 

[vcsharp2003]

The actual equation should read $$PV^x=P_0V_0^x$$What then?

I see, so right hand side is a constant if we raise both sides to $\frac{1}{x}$. Still we get $P_o^{\frac{1}{x}} V_o$, which should be a constant inspite of power involving x?

 

[Chestermiller]

I see, so right hand side is a constant if we raise both sides to $\frac{1}{x}$. Still we get $P_o^{\frac{1}{x}} V_o$, which should be a constant inspite of power involving x?

We rewrite it as $$\frac{V}{V_0}=\left(\frac{P_0}{P}\right)^{\frac{1}{x}}$$

 

[vcsharp2003]

We rewrite it as $$\frac{V}{V_0}=\left(\frac{P_0}{P}\right)^{\frac{1}{x}}$$

Ok. So LHS would be a constant for isochoric process. This would means the RHS is also the same constant, which is only possible if $x = -\infty$.

 

[Chestermiller]

Ok. So LHS would be a constant for isochoric process. This would means the RHS is also the same constant, which is only possible if $x = -\infty$.

Or $x=\infty$

 

[Frabjous]

polytropic processes are used for pedagogical purposes only.

You are too young. I remember reading reports that reported gamma for various types of rock for simulation in hydrocodes.

 

[Chestermiller]

You are too young. I remember reading reports that reported gamma for various types of rock for simulation in hydrocodes.

I’m 81.

 

[vcsharp2003]

Or $x=\infty$

Yes