vaibhav garg
- 16
- 0
In the adjoining figure if acceleration of M with respect to ground is a, then
A) Acceleration of m with respect to M is a
B) Acceleration of m with respect to ground is asin(α/2)
C) Acceleration of m with respect to ground is a
D) Acceleration of m with respect to ground is atan(α)
The 2nd question in the image below
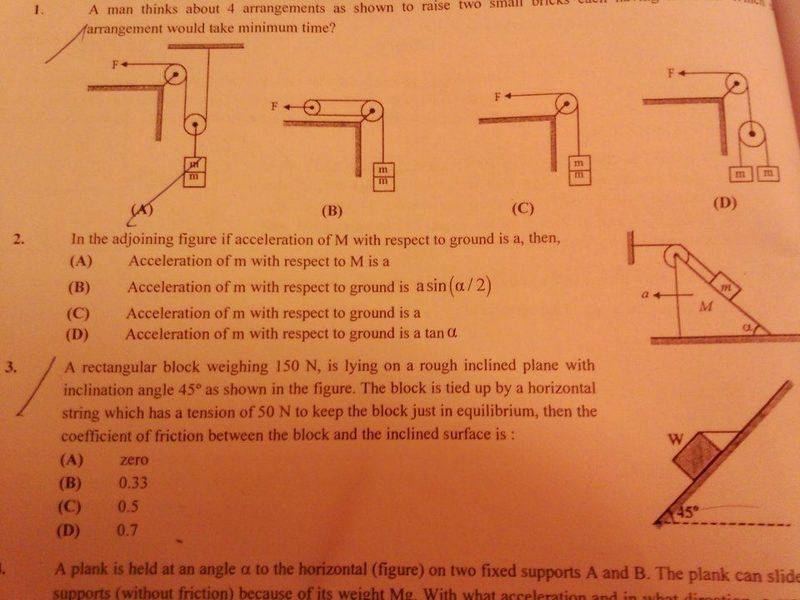
The acceleration of m in the vertical direction should be atan(α) by using length constant relation and in the horizontal direction it should be same as the wedge that is a. therefore the resultant should be asec(α), what am i doing wrong here ?
A) Acceleration of m with respect to M is a
B) Acceleration of m with respect to ground is asin(α/2)
C) Acceleration of m with respect to ground is a
D) Acceleration of m with respect to ground is atan(α)
The 2nd question in the image below
The acceleration of m in the vertical direction should be atan(α) by using length constant relation and in the horizontal direction it should be same as the wedge that is a. therefore the resultant should be asec(α), what am i doing wrong here ?
Last edited: