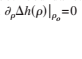Understanding the Notation: Deciphering the Equation in the Image

In summary, the conversation is about understanding an equation in an attached image. The equation involves a Monge parameterization height function, a boundary condition, and outer and inner boundaries. The conversation also discusses the best place to post the question and the possibility of using d/dp as the operator instead of d/dρ. Ultimately, the issue is resolved and the person is grateful for the help.
  • #1
lucdj3
4
0
Can you help me figure out what the equation in the attached image means?
What I do know is: h(p) is a Monge parameterization height function depending on radius (p), this is a boundary condition for a differential equation, and p0 is the outer boundary, with the inner boundary creating a boundary condition of h(pi)=0.
Thanks!
 

Attachments

  • biharmonicboundarycondition.png
    biharmonicboundarycondition.png
    598 bytes · Views: 580
Physics news on Phys.org
  • #2
I wasn't sure where this thread should be posted, so if there would have been a better place, please let me know and I will re-post there
 
  • #3
To me this read: The partial derivative with respect to ##\rho## evaluated at ##\rho=\rho_0##.
As in take the derivative first and then set ##\rho=\rho_0##.
I could be wrong though.
 
  • Like
Likes lucdj3
  • #4
That seems reasonable. Short term it is yielding something that doesn't look wrong, once I get through everything else I'll be able to tell if it's right. Thanks!
Any idea why it wouldn't be d/dp as the operator out front?
 
  • #5
Maybe the author is being sloppy because it looks like it only depends on ##\rho## and therefore it could be derived with ##\frac{d}{d\rho}##.
 
  • #6
Well it worked it, thanks!
 

FAQ: Understanding the Notation: Deciphering the Equation in the Image

What does "x" mean in this notation?

In mathematics, "x" is often used as a variable or placeholder for an unknown value. It can also represent a coordinate in a graph or a dimension in a geometric shape.

What does the superscript or subscript mean in this notation?

Superscripts and subscripts are used to indicate a power or index respectively. For example, "x2" means x squared and "x1" means x subscript 1.

What does the symbol "Σ" mean in this notation?

The symbol "Σ" is the Greek letter sigma, and in mathematics, it represents a summation or adding up of a series of numbers or variables.

What does the notation "f(x)" mean?

The notation "f(x)" is used in functions, where "f" represents the name of the function and "x" is the input or independent variable. It is read as "f of x" or "the value of f at x".

What does "∫" mean in this notation?

The symbol "∫" is called the integral sign and it represents the process of finding the area under a curve or the accumulation of a continuous function. It is often used in calculus and is read as "the integral of" or "the antiderivative of".

Similar threads

I Heat Equation: Solve with Non-Homogeneous Boundary Conditions
Replies
4
Views
2K
Question about initial and boundary conditions with the heat equation
Replies
1
Views
1K
Question about the classic Image Problem
Replies
3
Views
2K
A Green function issue: can bound. cond. be applied mode-wise?
Replies
1
Views
1K
Torque that a grounded infinite sheet exerts on a dipole
Replies
11
Views
248
Potential function of a flow around a stagnation point
Replies
19
Views
1K
I Understanding the dynamics of a perturbed quantum harmonic oscillator
Replies
3
Views
869
I Deciphering the Symbolic Shapes in Fundus Images: A Question on their Meaning
Replies
7
Views
2K
Magnetic field in and around a conductive hollow cylinder
Replies
2
Views
757
I Unraveling Laplace's Equation: Exploring Valid Domains and Boundary Conditions
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top