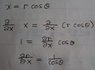You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Understanding the Reciprocal Form of Sin and Cos in Polar Coordinates
- Thread starter athrun200
- Start date
-
- Tags
- Coordinate Gradient Polar
Physics news on Phys.org
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
Hi athrun200! 
You seem to understand how to do multivariate calculus.
I didn't check all your equations, but they seem right.
However, you end up in an expression with i and j, when you should be ending up in an expression with \boldsymbol{e_{r}} and \boldsymbol{e_{\theta}}.
Perhaps you should make a substitution like that?
You seem to understand how to do multivariate calculus.
I didn't check all your equations, but they seem right.
However, you end up in an expression with i and j, when you should be ending up in an expression with \boldsymbol{e_{r}} and \boldsymbol{e_{\theta}}.
Perhaps you should make a substitution like that?
athrun200
- 275
- 0
In fact, the first term on my last step is very similar to \boldsymbol{e_{r}} and same for the second term. Can I really convert them to \boldsymbol{e_{\theta}} by substitution ?I like Serena said:However, you end up in an expression with i and j, when you should be ending up in an expression with \boldsymbol{e_{r}} and \boldsymbol{e_{\theta}}.
Perhaps you should make a substitution like that?
Sorry that I can't think of any substitution which is useful.
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
You're making a transition from cartesian coordinates to polar coordinates.
In your relevant equations section you have defined the relation between the unit vectors of the two sets of coordinates.
What you need is the inverse relation.
And in your attempt you switch the coordinates from cartesian to polar, which is good, but you also need to switch the unit vectors from cartesian to polar.Edit: I just checked a little bit of your equations, and I do not understand how you got \frac {\partial r} {\partial x} = \frac 1 {\cos \theta}.
That looks wrong.
In your relevant equations section you have defined the relation between the unit vectors of the two sets of coordinates.
What you need is the inverse relation.
And in your attempt you switch the coordinates from cartesian to polar, which is good, but you also need to switch the unit vectors from cartesian to polar.Edit: I just checked a little bit of your equations, and I do not understand how you got \frac {\partial r} {\partial x} = \frac 1 {\cos \theta}.
That looks wrong.
athrun200
- 275
- 0
I like Serena said:You're making a transition from cartesian coordinates to polar coordinates.
In your relevant equations section you have defined the relation between the unit vectors of the two sets of coordinates.
What you need is the inverse relation.
And in your attempt you switch the coordinates from cartesian to polar, which is good, but you also need to switch the unit vectors from cartesian to polar.
Edit: I just checked a little bit of your equations, and I do not understand how you got \frac {\partial r} {\partial x} = \frac 1 {\cos \theta}.
That looks wrong.
I obtain it like this. (I am also not sure about it.)
Attachments
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
Ah well, that is not right.
If you take the partial derivative on the right side, you need to apply the product rule, meaning you also have to differentiate theta.
If you do that, you'll not find it so easy to calculate dr/dx.
Instead I suggest you fill in r = \sqrt{x^2+y^2}, take the derivative, and simplify any way you like afterward.
You'll get a different result for \frac {\partial r} {\partial x} then, which is also why your end result is off by a factor 2.
If you correct this and the similar mistakes, you'll find the proper end result.
If you take the partial derivative on the right side, you need to apply the product rule, meaning you also have to differentiate theta.
If you do that, you'll not find it so easy to calculate dr/dx.
Instead I suggest you fill in r = \sqrt{x^2+y^2}, take the derivative, and simplify any way you like afterward.
You'll get a different result for \frac {\partial r} {\partial x} then, which is also why your end result is off by a factor 2.
If you correct this and the similar mistakes, you'll find the proper end result.
Last edited:
athrun200
- 275
- 0
I get the answer! Thx!I like Serena said:Ah well, that is not right.
If you take the partial derivative on the right side, you need to apply the product rule, meaning you also have the differentiate theta.
If you do that, you'll not find it so easy to calculate dr/dx.
Instead I suggest you fill in r = \sqrt{x^2+y^2}, take the derivative, and simplify any way you like afterward.
You'll get a different result for \frac {\partial r} {\partial x} then, which is also why you're end result is off by a factor 2.
If you correct this and the similar mistakes, you'll find the proper end result.
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
Good! And thanks for your thx. 
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 999
- Replies
- 2
- Views
- 2K
- Replies
- 14
- Views
- 3K
- Replies
- 22
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 96
- Calculus and Beyond Homework Help
-
Solving the wave equation with piecewise initial conditions
- Started by songoku
- Replies: 11
- Calculus and Beyond Homework Help
-
Area of loop in x-y plane
- Started by littlemathquark
- Replies: 20
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math