Miike012
- 1,009
- 0
Homework Statement
THIS PART I UNDERSTAND ( I am just adding it so the pic makes sence).
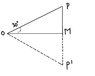
Let angle AOP traced out be 30 deg. Produce PM to P' making MP' equal to PM.
The two triangles OMP and OMP' have their sides OM and MP' equal to OM and MP and also the contained angles equal.
Therefore OP' = OP, and angle OP'P = angle OPP' = 60 deg.
That the triangle P'OP is equilateral
THIS IS WHERE I DONT UNDERSTAND:
Hence: OP^2 = PP'^2 = 4PM^2 = 4OP^2 - 4a^2
Where OM equals a.
3OP^2 = 4a^2
I understand why OP^2 = PP'^2 but how do they equal 4PM^2 = 4OP^2 - 4a^2 ?
And where did 3OP^2 = 4a^2 come from?