Using Centripetal Forces to find the radius of a circle

[QuickSkope]

Homework Statement

A 100g (0.1kg) rock is attatched to a 1.0m rope and spun around in a circle with a period of rotation of 1.0s. What is the Radius of the circle that it forms?

Homework Equations

Fc = (mV^2) / r
V= (2∏r/T)
LCosθ = r

The Attempt at a Solution

Im quite stick here, as I am not sure how I could ever find r without knowing the θ of the circle.

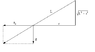
First thing I tried was making a triangle like so:

Illustration in 2D

Im going to start with the simple equation TCosθ = Fc. We also know that (mV^2)/r = Fc. If you put those 2 equations together, you get TCosθ = (mV^2)/r. This leaves us with the equation:

TCosθ = (mV^2)/ r

Furthurmore, we know that V = 2πr/P (Where P is period, should normally be T but there's Tension in this equation, so ill just do P)

TCosθ = m (2πr/P)^2 / r

The period of rotation is 1, so the equation simplifies again to:

TCosθ = m (2πr)^2 / r

We can also sub r into the formula we just moved in.

TCosθ = m (2π (Cosθ)^2) / Cosθ

From here, we can make the equation:

T = (m (2π) ^2 * (Cosθ)^2) / (Cosθ)^2 (Correct? I am not sure if that's logical)

Now the (Cosθ)^2 can cancel out, making:

T = m (2π)^2

Sub in the values, we have T = (0.1)(2π)^2
= 0.4π^2

We now know Tension, Which we can use in the triangle.

Triangle illustration

If I use Sin, I can find that the angle is 14.37321*.

We can use this θ in the equation LCosθ = r
(1)(Cos14.37321) = r
r = 0.97 m.

Is that correct?

 

[gneill]

Your method and result look fine.

Note that you might consider the problem in terms of similar triangles (I know, geometry was a looong time ago ).

Consider the ratio $g/a_c$...

You can use the rotational motion form for centripetal acceleration, $a_c = ω^2 r$, where $ω = 2\pi/T$. A little algebra and you can find an expression for r that does not require sines or cosines.

 

[QuickSkope]

Your method and result look fine.

Note that you might consider the problem in terms of similar triangles (I know, geometry was a looong time ago ).

Consider the ratio $g/a_c$...

You can use the rotational motion form for centripetal acceleration, $a_c = ω^2 r$, where $ω = 2\pi/T$. A little algebra and you can find an expression for r that does not require sines or cosines.

Do you mind explaining that a little? I'd like to check my answer, as I think 0.97m is a little large for the radius concidering you only make a full turn per minute. Or if you could do the math for this perticular situation and make sure it comes out correct, that would be awesome. Its for marks, so I just don't want to get it wrong.

Thanks :D

 

[gneill]

Do you mind explaining that a little? I'd like to check my answer, as I think 0.97m is a little large for the radius concidering you only make a full turn per minute. Or if you could do the math for this perticular situation and make sure it comes out correct, that would be awesome. Its for marks, so I just don't want to get it wrong.

Thanks :D

The problem says that the period of rotation is 1 second, not 1 minute. So ω is $2\pi/1sec$.

L is the length of the rope. r is the resulting radius of the circle that the mass follows at one revolution per second. $a_c$ is the centripetal acceleration acting on the rotating mass. g is the gravitational acceleration. You should be able to pick out similar triangles in the diagram. Equate the side-length ratios.

 

[QuickSkope]

Yea, sorry you're right. 1 second.

Ohh, so the Theta in both Triangle Ac/g and Lr are the same, correct? So you can equate the two, like this?

Tanθ = g/ac
Tanθ = √1^2 - r^2

g/ac = √ 1-r^2

g/ (2π)^2 = √ 1-r^2

(9.8 / (2π^2)) ^ 2 = 1-r^2

r^2 = 1 - (9.8 / (2π^2)) ^ 2

r^2 = .938

r= .969

Thats what I get when I do similar triangles, which I am 99% sure isn't right. Is the g (.1)(9.8) or mg, or is it just 9.8?

 

[haruspex]

is the g (.1)(9.8) or mg, or is it just 9.8?

It's g, not mg. The mass canceled out.

 

[QuickSkope]

Alright, so that makes both of them the same answer :). I end up with 0.97. Can someone do it and verify that that is right?

Thanks :)

 

[haruspex]

Alright, so that makes both of them the same answer :). I end up with 0.97. Can someone do it and verify that that is right?

Thanks :)

I agree with .97

 

[QuickSkope]

Great, thanks :D