Using Conservation of Energy to Analyze a Potential Energy Graph

AI Thread Summary
The discussion focuses on analyzing a potential energy graph using the conservation of energy principle. The user is struggling to relate time to the graph and connect force, mass, and acceleration equations. They express frustration with deriving velocity from the potential energy and determining the turning point of motion. Key questions include how to calculate velocity at various positions and what type of motion to expect based on these calculations. The conversation emphasizes the need to integrate energy concepts with kinematic equations for a comprehensive understanding.
chuuke
Messages
3
Reaction score
1

Homework Statement


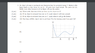
I'm trying to figure out how to do D) and relate time to this potential energy graph.
Screenshot (27).png


Homework Equations


All I really know is that F = -dU/dx

The Attempt at a Solution


I tried to do something with F = ma
and a = d2x/ dt2
and then set the - derivative of U(x) equal to the above equation
but I can't really get an answer, and am quite frustrated cause I don't know how to go about answering this.
 

Attachments

  • Screenshot (27).png
    Screenshot (27).png
    18.5 KB · Views: 1,793
Physics news on Phys.org
You need to use the conservation of energy. When released from B, what is going to be the velocity at any point? How is that related to position?

Also, what position do you have as the turning point? Based on that, what kind of motion do you expect?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Graphing Elastic Potential Energy
Replies
10
Views
2K
Is potential energy defined only for internal conservative forces?
Replies
15
Views
1K
Force components for mass attached to two springs
Replies
15
Views
1K
Expression for magnitude of the constant friction force
Replies
7
Views
955
Conservation of Momentum Problem - Mechanical and Kinetic Energies
Replies
2
Views
899
Is the line integral of tangential force in pendulum equal to the negative of change in potential energy?
Replies
3
Views
824
Conservation of Energy with Gravitational Potential Energy
Replies
6
Views
2K
Elastic potential energy - different methods, different results
Replies
2
Views
771
Minimizing the Energy of Two Conductors Very Far Apart
Replies
23
Views
1K
Potential energy of ball thrown upwards
Replies
5
Views
14K

Hot Threads

Recent Insights

Back
Top