Vector calculus for ellipse in polar coordinates

[dragonxhell]

Hello =]
I'm having trouble with this question, can somebody please help me with it! I'll thanks/like your comment if help me =)

![Question][1]

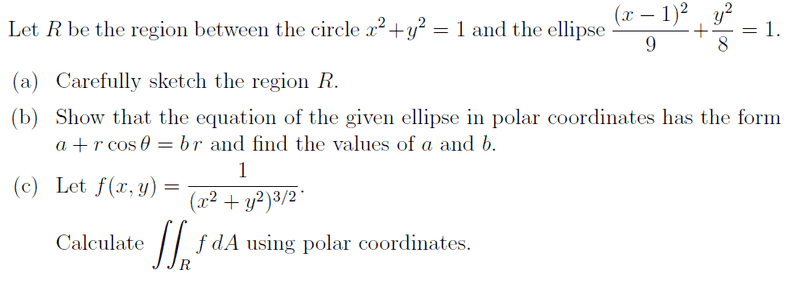
I know that for a ellipse the parametric is x=a sin t , b= b cos t t:0 to 2pi (?)

for part a) I drew up the graph but not sure if it's right. the circle have 1 radius and for the ellipse I able to find the x= 2
(x-1)^2 =9
sqrt(x-1)^2=sqrt9
x-1=3
x=4

for y=2sqrt2
y^2=8
sqrty=sqrt8
y=sqrt4 sqrt 2
y= 2sqrt2 or 2.8

So the region should be the circle? since the ellipse like cover the whole circle?
Thank you very much for helping!
Cheers.

 

[CAF123]

I know that for a ellipse the parametric is x=a sin t , b= b cos t t:0 to 2pi (?)

That would be valid if the ellipse was centered at the origin, which is not the case here. (but only a slight adjustment needs to be made).

for part a) I drew up the graph but not sure if it's right. the circle have 1 radius and for the ellipse I able to find the x= 2
(x-1)^2 =9
sqrt(x-1)^2=sqrt9
x-1=3
x=4

for y=2sqrt2
y^2=8
sqrty=sqrt8
y=sqrt4 sqrt 2
y= 2sqrt2 or 2.8

There exists two solutions to each of these equations.

So the region should be the circle? since the ellipse like cover the whole circle?
Thank you very much for helping!
Cheers.

The region is not exactly a circle, but the unit circle is completely contained within the ellipse.

 

[dragonxhell]

That would be valid if the ellipse was centered at the origin, which is not the case here. (but only a slight adjustment needs to be made).
There exists two solutions to each of these equations.


The region is not exactly a circle, but the unit circle is completely contained within the ellipse.
the region happen is when 2 of graph meet each other?

so for x it's 4 and -4 and for y its 2sqrt2 and -2sqrt 2 right?
i did a sketch of it, by any chance you know how to do this question? =(


Mod note: The image was way too large. Please scale the image down to about 900 x 600 pixels and edit this post to include it again, or add it in a new post in this thread.

 

[CAF123]

so for x it's 4 and -4 and for y its 2sqrt2 and -2sqrt 2 right?

No, for the first equation, you solve $(x-1)^2 = 9$ so $x-1 = \pm 3$ What are the two solutions?
Similarly for the other equation.

Your sketch shows the ellipse concentric with the unit circle, but this is incorrect since the ellipse has a centre (1,0). When you find the correct solutions to the above, it should fix things.

 

[LCKurtz]

@dragonxhell: To get started on this problem you need to substitute the polar coordinate values for $x$ and $y$ into the equation of the ellipse and solve it for $r$. That should lead you to the answer for part b. Then you will use the form$$
\int_0^{2\pi} \int_{r_{inner}}^{r_{outer}} \frac 1 {r^3}r\,drd\theta$$

 

[dragonxhell]

No, for the first equation, you solve $(x-1)^2 = 9$ so $x-1 = \pm 3$ What are the two solutions?
Similarly for the other equation.

Your sketch shows the ellipse concentric with the unit circle, but this is incorrect since the ellipse has a centre (1,0). When you find the correct solutions to the above, it should fix things.

o so the centre is (1,0) and the equation you show me I have already obtained
But don't you move the 1 over? To just simply get x by it self? So it should be 4 and -3 (-4+1?)

 

[dragonxhell]

@dragonxhell: To get started on this problem you need to substitute the polar coordinate values for $x$ and $y$ into the equation of the ellipse and solve it for $r$. That should lead you to the answer for part b. Then you will use the form$$
\int_0^{2\pi} \int_{r_{inner}}^{r_{outer}} \frac 1 {r^3}r\,drd\theta$$

Is this right? Can somebody double check this for me? It seem right to me...


(x−1)²/9 + y²/8 = 1
8(x−1)² + 9y² = 72
8x² − 16x + 8 + 9y² = 72
9(x²+y²) − x² − 16x + 8 = 72
9(x²+y²) = x² + 16x + 64
9(x²+y²) = (x + 8)²
9r² = (r cosθ + 8)²3r = r cosθ + 88 + r cosθ = 3r
a = 8, b = 3
c)R is region outside circle: r = 1*and inside ellipse: r = 8/(3−cosθ)
Limits:*1 ≤ r ≤ 8/(3−cosθ)
0 ≤ θ ≤ 2πƒ
= 1/(x²+y²)^(3/2)
= 1/(r²)^(3/2)
= 1/r³∫∫ ƒ dA = ∫ [0 to 2π] ∫ [1 to 8/(3−cosθ)] 1/r³ * r dr dθR. . . . .
= ∫ [0 to 2π] ∫ [1 to 8/(3−cosθ)] 1/r² dr dθ. . . . .
= ∫ [0 to 2π] (−1/r) | [1 to 8/(3−cosθ)] dθ. . . . .
= ∫ [0 to 2π] (−(3−cosθ)/8 − (−1)) dθ. . . . . = ∫ [0 to 2π] 1/8 (cosθ + 5) dθ. . . . .
= 1/8 (sinθ + 5θ) | [0 to 2π]*. . . . .
= 1/8 [(0 + 10π) − (0 + 0)]. . . . .
= 5π/4

Also for part a) the R region it is the region between the ellipse to the circle right?

 

[LCKurtz]

Is this right? Can somebody double check this for me? It seem right to me...


(x−1)²/9 + y²/8 = 1
8(x−1)² + 9y² = 72
8x² − 16x + 8 + 9y² = 72
9(x²+y²) − x² − 16x + 8 = 72
9(x²+y²) = x² + 16x + 64
9(x²+y²) = (x + 8)²
9r² = (r cosθ + 8)²3r = r cosθ + 88 + r cosθ = 3r
a = 8, b = 3
c)R is region outside circle: r = 1*and inside ellipse: r = 8/(3−cosθ)
Limits:*1 ≤ r ≤ 8/(3−cosθ)
0 ≤ θ ≤ 2πƒ
= 1/(x²+y²)^(3/2)
= 1/(r²)^(3/2)
= 1/r³∫∫ ƒ dA = ∫ [0 to 2π] ∫ [1 to 8/(3−cosθ)] 1/r³ * r dr dθR. . . . .
= ∫ [0 to 2π] ∫ [1 to 8/(3−cosθ)] 1/r² dr dθ. . . . .
= ∫ [0 to 2π] (−1/r) | [1 to 8/(3−cosθ)] dθ. . . . .
= ∫ [0 to 2π] (−(3−cosθ)/8 − (−1)) dθ. . . . . = ∫ [0 to 2π] 1/8 (cosθ + 5) dθ. . . . .
= 1/8 (sinθ + 5θ) | [0 to 2π]*. . . . .
= 1/8 [(0 + 10π) − (0 + 0)]. . . . .
= 5π/4

Also for part a) the R region it is the region between the ellipse to the circle right?

Yes. Very nice.

 

[dragonxhell]

Yes. Very nice.

Can you please check this question for me because my answer is different to my friends and they say its wrong...
Given the equation: G= (x^3 -3xy^2)I +(y^3-3x^2y)j +2k is conservative find the potential function for the fields that are conservative
My answer
f:grad f=F
fx=x^3-3xy^2
fy=y^3-3x^2y
fz=z

integral (x^3-3xy^2)dx
=x^4/4-3x^2y^2/2 +h(y, z)
fy or f'y= -3x^2 y +hy(y, z)
fy=y^3-3x^2y= -3x^2y+hy(y, z)
hy(y,z)=y^3

Integral y^3 dy = y^4/4 +gz
fz=0 because no z term ^
Integral 0dz =c
F= x^4/4-3x^2y^2/2 +y^4/4+c <-potential function

 

[LCKurtz]

Can you please check this question for me because my answer is different to my friends and they say its wrong...
Given the equation: G= (x^3 -3xy^2)I +(y^3-3x^2y)j +2k is conservative find the potential function for the fields that are conservative
My answer
f:grad f=F

There is no F anywhere. Don't you mean grad f = G?

fx=x^3-3xy^2
fy=y^3-3x^2y
fz=z

Is $f_z = z$ or $f_z = 2$? Look at G.

integral (x^3-3xy^2)dx
=x^4/4-3x^2y^2/2 +h(y, z)
fy or f'y= -3x^2 y +hy(y, z)
fy=y^3-3x^2y= -3x^2y+hy(y, z)
hy(y,z)=y^3

Integral y^3 dy = y^4/4 +gz
fz=0 because no z term ^
Integral 0dz =c

Poorly written. At this point you have$$
f = \frac {x^4} 4 - \frac {3x^2y^2} 2 +\frac{y^4} 4 + h(z)$$
Now you need to take $f_z$ and set it equal to the third term, whether it is a $2$ or a $z$. You don't get $f_z=0$ either way.

 

[dragonxhell]

There is no F anywhere. Don't you mean grad f = G?



Is $f_z = z$ or $f_z = 2$? Look at G.

Poorly written. At this point you have$$
f = \frac {x^4} 4 - \frac {3x^2y^2} 2 +\frac{y^4} 4 + h(z)$$
Now you need to take $f_z$ and set it equal to the third term, whether it is a $2$ or a $z$. You don't get $f_z=0$ either way.

sorry I type it all up on my phone and when I submit it it's so messy...
so you are saying
my integral y^4/4 must equal to fz which is z
So the final answer is
F=x^4/4 -3x^2y^2/2 +y^4/4 +z^2/2