borovecm
- 13
- 0
Vector proof that diagonals of rhomb split in ratio 1/2.
Hi. For my math homework I have to prove with vectors(we are currently learning that) that diagonals of any rhomb split in half in ratio 1/2.
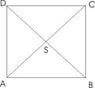
A,B,C,D are end points of rhombus, and S is point where diagonales AC and BD meet.
My goal is to get this 2 equations:
\vec{AS}=\stackrel{1}{2}*\vec{AC}
and
\vec{BS}=\stackrel{1}{2}*\vec{BD}
condition of rhomb:
\vec{AB}=\vec{DC}
\vec{AD}=\vec{BC}
\vec{AB}+\vec{BC}+\vec{CD}+\vec{DA}=\vec{0}
\vec{AS}+\vec{SD}+\vec{DA}=\vec{0}
\vec{AC}+\vec{CD}+\vec{DA}=\vec{0}
_______________________________
\vec{AC}+\vec{CD}-\vec{AS}-\vec{SD}=\vec{0}
\vec{AC}-\vec{AS}+\vec{BA}-\vec{SD}=\vec{0}
\vec{AC}+\vec{SA}+\vec{DS}+\vec{BA}=\vec{0}
\vec{AC}+\vec{DS}+\vec{SA}+\vec{BA}=\vec{0}
and I don't know if I am on the right track and I wan't your opinion.
Homework Statement
Hi. For my math homework I have to prove with vectors(we are currently learning that) that diagonals of any rhomb split in half in ratio 1/2.
Homework Equations
A,B,C,D are end points of rhombus, and S is point where diagonales AC and BD meet.
My goal is to get this 2 equations:
\vec{AS}=\stackrel{1}{2}*\vec{AC}
and
\vec{BS}=\stackrel{1}{2}*\vec{BD}
condition of rhomb:
\vec{AB}=\vec{DC}
\vec{AD}=\vec{BC}
\vec{AB}+\vec{BC}+\vec{CD}+\vec{DA}=\vec{0}
The Attempt at a Solution
\vec{AS}+\vec{SD}+\vec{DA}=\vec{0}
\vec{AC}+\vec{CD}+\vec{DA}=\vec{0}
_______________________________
\vec{AC}+\vec{CD}-\vec{AS}-\vec{SD}=\vec{0}
\vec{AC}-\vec{AS}+\vec{BA}-\vec{SD}=\vec{0}
\vec{AC}+\vec{SA}+\vec{DS}+\vec{BA}=\vec{0}
\vec{AC}+\vec{DS}+\vec{SA}+\vec{BA}=\vec{0}
and I don't know if I am on the right track and I wan't your opinion.
Attachments
Last edited: