(Vector statics) Effect of a pulley on free body diagram?

[dmk90]

For example, a 1-m bar fixed to a wall holding a weight of 100 N, like this:

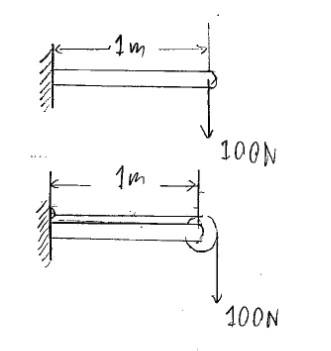
How will the free body diagram of the second case different from the first?

 

[PhanthomJay]

Axial load In beam (compression).

 

[dmk90]

Axial load In beam (compression).

Can you explain what the magnitude of that force would be, and why?

 

[PhanthomJay]

Can you explain what the magnitude of that force would be, and why?

As always, use free body diagrams and the equilibrium equations. The tension in a rope passing through an ideal pulley is the same on both sides of the pulley. So the force of the wall on the rope must have a magnitude of T, acting left. By summing external forces of the system in the x direction = 0, the horizontal force of the wall on the beam must also be T, acting right, since that it is the only place where another external force can exist. The shear and moment values in the beam are the same as in the first case.

Alternatively, you can draw a free body diagram of the pulley to identify the direction of the tension forces down and left, then a free body diagram of the beam without the pulley must show the same horizontal and vertical forces acting on it down and left. This gives the same result for beam forces and moments, but now their is an additional axial force in the beam, equal to _??__ N.