Vectors and angles word problem

[joedango]

A snow-covered ski slope makes an angle of θslope = 29.0° with the horizontal. When a ski jumper plummets onto the hill, a parcel of splashed snow is thrown up to a maximum displacement of 1.70 m at θsnow = 19.0° from the vertical in the uphill direction as shown in the figure below.

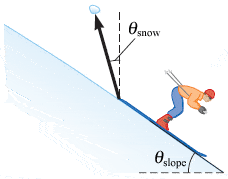
(a) Find the component of its maximum displacement parallel to the surface.

(b) Find the component of its maximum displacement perpendicular to the surface.

I don't know what component is parallel to the surface. I also don't know where the 1.70m goes

 

[RTW69]

I believe that 1.7 m is the length of the vector with the little snow ball on top of it. Create vectors parallel and perpendicular to the slope for the 1.7 meter vector