Vectors using the component method

AI Thread Summary
To add vectors using the component method, first calculate the x-component by multiplying the magnitude by the cosine of the angle, resulting in 2.56 for the i component. For the y-component, use the sine function: multiply the magnitude by sin(31.5°) to find the j component. The resultant vector can then be expressed in unit-vector notation as ...i + ...j. Clarification on the sine calculation for the y-axis is requested for further assistance. Accurate calculations are essential for determining the correct resultant vector.
farhana21
Messages
7
Reaction score
0
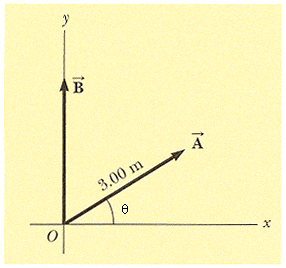
Use the component method to add the vectors and shown in the figure. The length of is 2.55 m and the angle θ = 31.5°. Express the resultant + in unit-vector notation.

The answer should be in the form of ...i + ...j

so far i have done

3*cos(31.5) = 2.56 so this is for ...i but I am unsure of how to find vector j for the y axis.

Please could someone advise me. All help and guidance given is much appreciated

vector.gif
 
Physics news on Phys.org

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Can A Vector Have Components Of Say Y or Z in the X-Hat Direction?
Replies
8
Views
857
Adding Vectors Using the Component Method
Replies
12
Views
11K
Calculate electric force using Coulomb's law (vector components are the struggle)
Replies
3
Views
1K
Vectors using the component method
Replies
3
Views
1K
Syntax Error? x and y components of E field in unit vector form
Replies
13
Views
2K
Confusion with force components
Replies
21
Views
2K
Inelastic 2D Collision with Vector Components
Replies
7
Views
2K
Am I Calculating the Components of V3 Correctly?
Replies
9
Views
2K
The components of force and velocity vectors in circular motion
Replies
11
Views
3K
Help about the unit vectors for polar coordinates in terms of i and j
Replies
13
Views
2K

Hot Threads

Recent Insights

Back
Top