Vertical Velocity Graph versus Time on a Slope

[mancity]

Homework Statement

A soccer ball is kicked up a hill with a flat top, as shown. The ball bounces twice on the hill, at the points shown, then lands on the top and begins rolling horizontally. Which of the following shows the vertical component of its velocity as a function of time?
Attached is the picture, along with the answer choices.

Relevant Equations

KE+PE=ME

I understand that through process of elimination the only plausible solution is (E), but a question that rises up:

When the ball bounces, does the velocity change from negative to positive instantly (as shown by the dotted lines) or gradually (a very small time period, but still solid line)?

 

[Orodruin]

The answer depends on how ideally you model the bounce. Of course, in the real world, the collision occurs smoothly over some time.

 

[Steve4Physics]

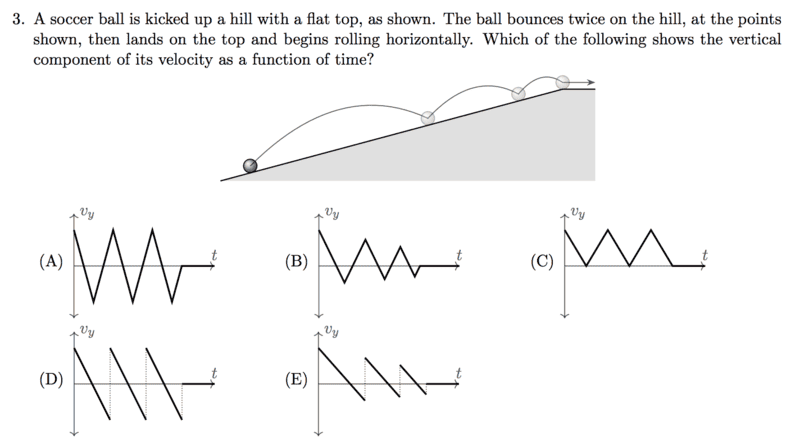
When the ball bounces, does the velocity change from negative to positive instantly (as shown by the dotted lines) or gradually (a very small time period, but still solid line)?

Not instantly, but over some (typically very small) time-interval. A solid, very steep line during each impact would have been better.

Also, there should be no 'sharp corners’ where two straight line-sections meet; the junction should be rounded. Motion is continuous - no discontinuities.

But it is common to simplify graphs for convenience.