Very difficult mechanics problem with friction

[Bestfrog]

Homework Statement

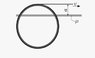
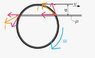
A hollow cylinder with mass m and radius R stands on a horizontal surface with its smooth flat end in contact the surface everywhere. A thread has been wound around it and its free end is pulled with velocity v in parallel to the thread. Find the speed of the cylinder. Consider two cases: (a) the coefficient of friction between the surface and the cylinder is zero everywhere except for a thin straight band (much thinner than the radius of the cylinder) with a coefficient of friction of μ, the band is parallel to the thread and its distance to the thread a<2R (the figure shows a top-down view); (b) the coefficient of friction is μ everywhere. Hint: any planar motion of a rigid body can be viewed as rotation around an instant centre of rotation, i.e. the velocity vector of any point of the body is the same as if the instant centre were the real axis of rotation.

The figure: http://i64.tinypic.com/2ijrv53.jpg

Homework Equations

The Attempt at a Solution

I have no idea were to start! I know that it is against the forum rules.. but can someone give me only a hint to set up the solution?

 

[Bestfrog]

The figure

 

[haruspex]

give me only a hint to set up the solution?

I take it we are to assume steady state, i.e. the cylinder moves to the right at constant speed.
For a), how many forces are there? What can you say about their magnitudes and directions? What equations can you write relating them?

 

[Bestfrog]

I take it we are to assume steady state, i.e. the cylinder moves to the right at constant speed.
For a), how many forces are there? What can you say about their magnitudes and directions? What equations can you write relating them?

There are three forces. One that pull the thread (its magnitude is $F_c = m \frac{v^2}{R}$). The other 2 are the frictions forces acting on the other direction (in the left), $f= dm.g. \mu$ with $dm$ the infinitesimal mass of the cylinder in contact with the friction line. I think that the forces make a torque (is it possible?)

 

[haruspex]

its magnitude is $F_c = m \frac{v^2}{R})$

I have no idea how you arrive at that. It is not a centripetal force. The speed is constant, so it can be any value for the same force. Anyway, its magnitude does not matter.

The other 2 are the frictions forces acting on the other direction

Not quite.
Kinetic friction acts to oppose the relative motion of the surfaces in contact. As the cylinder moves to the right and rotates, what is the direction of the relative motion between the cylinder and the table at those two points?

 

[Bestfrog]

I have no idea how you arrive at that. It is not a centripetal force. The speed is constant, so it can be any value for the same force. Anyway, its magnitude does not matter.

Ok I'm totally wrong :D

Not quite.
Kinetic friction acts to oppose the relative motion of the surfaces in contact. As the cylinder moves to the right and rotates, what is the direction of the relative motion between the cylinder and the table at those two points?

So the situation is this

 

[haruspex]

So the situation is this

Yes. Can you find the actual components of the relative velocities at the frictional points in terms of v, R, a and ω?

 

[Bestfrog]

Yes. Can you find the actual components of the relative velocities at the frictional points in terms of v, R, a and ω?

I'm struggling but I can't find any idea. For relative velocities you mean with respect to the ground?
For the velocity (not angular) I'm thinking that all the velocity vectors at a certain distance from the centre are equal to the vector of $v_{CdM}$ (i.e. At a distance $R-a$ the sum of the two vectors of the two points of the cylinder in contact with the ground is $v_{CdM}$). So $v_{a,dx} + v_{a,sx} = v_{CdM}$

 

[haruspex]

For relative velocities you mean with respect to the ground?

Yes.

For the velocity (not angular) I'm thinking that all the velocity vectors at a certain distance from the centre are equal to the vector of $v_{CdM}$ (i.e. At a distance $R-a$ the sum of the two vectors of the two points of the cylinder in contact with the ground is $v_{CdM}$). So $v_{a,dx} + v_{a,sx} = v_{CdM}$

I am unable to guess your notation.
Consider the motion of the cylinder as the sum of a linear motion, speed u say, and a rotation at rate ω. What equation relates some or all of u, ω, R, a and v?
Consider, e.g., the right-hand frictional point of the cylinder. That has x and y components of motion, x being parallel to the thread.
What contributions to its x and y velocities come from u (easy)?
Now ignore u. What contributions to its x and y velocities come from ω?