Vibration of Rigid Body with One Spring: Understanding Torque Equations

[Alex Santos]

Homework Statement

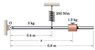
Rigid body with one spring.

Homework Equations

Torque equations ( M=I * "alpha")

The Attempt at a Solution

So I think I can solve this problem but there is only one thing I do not understand.

When I am writing my torque equation I would think that the weight of the bar and the cube would affect the torque
M = I * a + Mb * g *0.4 cos (theta) + Mw * g * 0.4 cos (theta) - k*0.4sin(theta) *0.4 cos(theta)
but apparently the equation should be
M = I*a -k*0.4sin(theta)*0.4cos(theta)

why does the mg of both the objects not affect the torque, whenever I try to include them the differential equation becomes unsolveable

 

[rock.freak667]

From the equilibrium position, your forces would be along the lines of kδ=mgcosθ (component of the weight)

So that when the mass is displaced again by some distance x, the spring force becomes k(x+δ). And the weight cancels out.

 

[Alex Santos]

Alright thanks for the answer. Think I understand this now :)