- #1
Rightwrong
- 6
- 0
I1. Homework Statement
A cylindrical vessel whose diameter and height both are equal to 30 cm is placed on a horizontal surface and a small particle p is placed in it at a distance of 5 cm from the centre. An eye is placed at a position such that the edge of the bottom is in the plane of drawing. Upto what minimum height should water be filled in the vessel to make particle p visible?
Apparent depth (d’) = real depth (d) / refractive index
My answer is 40 cm which is wrong.
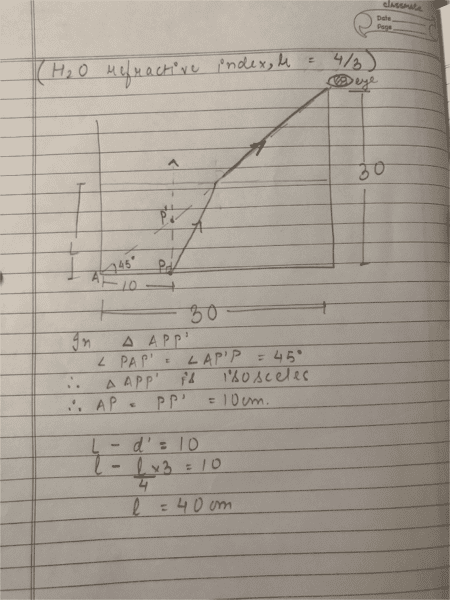 [/B]
[/B]
A cylindrical vessel whose diameter and height both are equal to 30 cm is placed on a horizontal surface and a small particle p is placed in it at a distance of 5 cm from the centre. An eye is placed at a position such that the edge of the bottom is in the plane of drawing. Upto what minimum height should water be filled in the vessel to make particle p visible?
Homework Equations
Apparent depth (d’) = real depth (d) / refractive index
The Attempt at a Solution
My answer is 40 cm which is wrong.
Attachments
Last edited by a moderator:
