Viscosity of oil at various temperatures

[nvidia17]

I'm trying to work out the viscosity of oil at various temperatures. I've got all my results, but when I try to work out the viscosity I get some really far out answers. What region would you expect the viscosity of oil room temperature to be? I get this result for viscosity of oil: -1330245.26.

This is the formula I'm using.

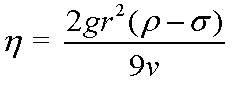
I've found the density of the steel ball bearing to be 7545.4kg/m3 and the density of oil to be 168.8kg/m3.

I know the working out of the velocity is correct, at 0.44m/s¹

The radius of the ball bearing is 0.0061m
What looks out of place here?

This is my A2 coursework, so tips or help would be appreciated. :shy:

 

[nvidia17]

Okay, I'm sorry for this, but it turns out I made an error in my formula's Excel. I double checked them with a calculater and realized that I hadn't put the radius in metres, but mm.

Sorry for the inconvenience.