Voltage measured across a capacitor with embedded charges

[Barloud]

Hi all,

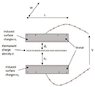
Lets consider the situation illustrated in the attached figure. A permanent surface charge density \sigma is embedded in between the two metallic electrodes of a capacitor. \sigma is located at distances d1 and d2 from the bottom and top electrodes, respectively. \sigma induces a charge unbalance in the metallic electrodes. Ignoring stray fields, the surface charge density \sigma_{t} induced on the bottom surface of the top electrode can be computed by applying the principle of (dis)continuity of the dielectric displacement in the gap and the definition of the voltage V across the electrodes. Assuming vacuum in between the electrodes, one obtains \sigma_{t} =\frac{\epsilon_{0}V-d1\sigma}{d1+d2}. The same can be done for the surface charge \sigma_{b} induced on the top surface of the bottom electrode. The total charges Q_{t} and Q_{b} accumulated on the facing surfaces of the two electrodes is obtained by integrating \sigma_{t} and \sigma_{b}, respectively. We have simply Q_{t}=\sigma_{t} WL and Q_{b}=\sigma_{b} WL.

Imagine now that we connect the two electrodes to an electrometer. The input impedance of such a system can be reasonably approximated by a capacitance C. Here comes my question: what would be the potential difference measured by the electrometer? For a simple capacitor, one should compute the charges Q on the electrodes and use the basic formula Q=CV but my problem here is that the charges on the top and bottom electrodes,Q_{t} and Q_{b}, are not equal in magnitude and opposite in sign, as in the simple capacitor case.

 

[DarioC]

Your diagram shows V with an arrow. What does that mean? The wires both have positive charges. Are they connected together to the same source?

 

[Barloud]

Well, the arrow on V means that it is the potential difference between the top and bottom electrode (and not the opposite). There is no external source of voltage in the system I describe.

The + charges that I have drawn in the wires are just the results of the imbalance created by the permanent charges in between the plates. In other words, the permanent charges in between the plates attracts negative charges on both metal plates. The permanent charges also repulse positive charges on both plates (the metal has to remain neutral over its volume)...or am I totally wrong in my understanding?

 

[DrZoidberg]

As long as the distance between the plates is small relative to the plates sizes i.e. as long as the field is homogenous, \sigma_{t} and \sigma_{b} are going to be the same. They will each be exactly \frac{\sigma}{2}
So you can simply model your capacitor as two capacitors in series each with a charge of \frac{Q}{2}

 

[DarioC]

Ah, thank you for introducing me to a entirely new (to me) concept. Electrets. Wow, interesting.
Fits right in with my curiosity on the concept of "free" electrons.

 

[Barloud]

As long as the distance between the plates is small relative to the plates sizes i.e. as long as the field is homogenous, \sigma_{t} and \sigma_{b} are going to be the same. They will each be exactly \frac{\sigma}{2}
So you can simply model your capacitor as two capacitors in series each with a charge of \frac{Q}{2}

Lets assume that the electrodes are shorted together (V=0) and forget the story about the electrometer for the moment. Just look at the equations and you will see that the charges on the two plates are not equal in magnitude and opposite in sign. The situation I describe goes a bit beyond the analysis of classical capacitors.

Back to the case where a "classical" capacitor is connected to the two electrodes:

So you can simply model your capacitor as two capacitors in series each with a charge of \frac{Q}{2}

Which Q then? Qt or Qb? :)

DarioC, indeed, I am talking about electrets.

 

[DarioC]

Ah, now is see the key to your question. D1/D2...and I thought this was over my head. Chuckle. The point would be that you have a more concentrated collection of positive charges on one plate "surface" than the other, which if your electrometer has infinite resistance should (I think) give a voltage indication.

Is the distribution offset you describe a normal characteristic of electrets or is this a thought experiment?

 

[DrZoidberg]

When you short the electrodes the situation changes completely.
You can model the two cases with circuits consisting of capacitors.
If the electrodes are not connected the model would consist of 4 capacitors. The two in the middle and then two very small ones that represent the capacity of the electrodes relative to ground.
If you short the electrodes you only need 3 capacitors.
Here is a diagram.

Cg is always much smaller then Ct and Cb.
If you now let some charge flow into the connection between Ct and Cb e.g. by connecting a battery between that point and ground, you should see that you get approximately the same amount of charge on both capacitors in the first case but very different amounts in the second case.

Just look at the equations and you will see that the charges on the two plates are not equal in magnitude and opposite in sign.

You mean this equation?
\sigma_{t} =\frac{\epsilon_{0}V-d1\sigma}{d1+d2}
If d2 is 0 then according to your equation \sigma_{t} would also be 0. So despite directly touching the top electrode, no charge is induced?

 

[Barloud]

Mmmhhh, thanks for your answer DrZoidberg, I need to think about it. The capacitances to ground may be what I missed. I have always difficulties to relate the field and circuit descriptions of an electrical problem (and even more to relate both description to reality).

DarioC, the offset I describe is often a real characteristic of electret based devices (but it can be avoided depending on the design).