- #1
Lim Y K
- 26
- 0
Homework Statement
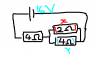
In a circuit consisting of both parallel and series arrangement, how do you find the potential difference of X(in red) and Y(in blue)? and how did you derive at those answers?
Homework Equations
idk
The Attempt at a Solution
total resistance=4 ohms +(1/r eff=1/2ohms+1/4ohms)
=4ohms+4/3ohms
=5 1/3 ohms
current=16 divide by 5 1/3ohms
=3 ampere
potential diff for X ------V=RI
=(1/2)(3)
=1.5
potential diff for Y-------V=RI
=(1/4)(3)
= 3/4
I WAS TOLD THOSE IN RED ARE WRONG. BUT WHY? I DIDN'T SEE ANY MISTAKE IN CALCULATION.
can someone help me please? please explain to me what went wrong thanks