W. Mathematica 8 stays running and does not evaluate

[SCC10]

Hi

I am a user of Mathematica as a tool for calculation in Structural Mechanics. I had a problem recently in the integration of expressions a bit long, and honestly I do not understand what might be causing the slowdown.

I want to just evaluate this:

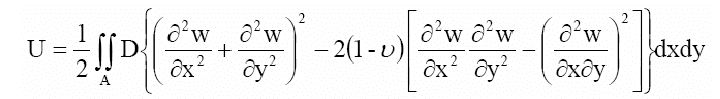
This is for the Raileygh-Ritz method for rectangular plates. Then, i use the following code:

U=(1/2)*D1*Integrate[((D[W,{x,2}]+D[W,{y,2}])^2-2*(1-v)*(D[W,{x,2}]*D[W,{y,2}]-(D[W,x,y]^2))), {x, -a, a}, {y, 0, b}]

, were W is function of x and y


The problem is that the program continues running without answering over several minutes.
Anyone have any solution or advise that could make my process more agile?

Thank you in advance!

 

[phyzguy]

The symbolic integration of Integrate can take a very long time for complex functions, and in fact may never find an answer. If you know the values of all of the parameters, NIntegrate will run much faster and always will return an answer. You will need to assign all of the parameters beforehand, so that NIntegrate is just dealing with numbers, not symbolic expressions. I don't know if this is possible for you or not.

If you can't use NIntegrate, you might try Simplify on the symbolic expression before you use Integrate. Sometimes this helps.

 

[jackmell]

Anyone have any solution or advise that could make my process more agile?

Thank you in advance!

Yep.

(1) We have a sub-forum "Computing and Tech/Math and Science software" down below. They're really good. Maybe this should be moved to that.

(2) No doubt in my mind even if the assignment was to find an analytic solution and I couldn't after some effort, I'd try and numerically solve it with just any old reasonable values for the necessary parameters, just to get a handle on it. In that case, use NIntegrate to see what's up.

(3) Re-cast the problem entirely in terms of a Mathematica problem and NIntegrate, try and solve it, if you run into problems, post a thread in the Science software forum describing where you're having problems.

 

[Bill Simpson]

The problem is that the program continues running without answering over several minutes.

Attach the simplest notebook you can which includes the definition of W

 

[SCC10]

Thank you for the answers

I have a problem with using the command NIntegrate, is that later I will need the W again for other calculations and for this reason I need to use symbolic integration.

Here is the nb whit the definition of W, Wxy in case


Sorry about the location of the post, I am new here... Can any moderator move the topic to the correct location?

Thanks!

 

[Bill Simpson]

Part of the reason it is taking so long is that your integrand
((D[Wxy,{x,2}]+D[Wxy,{y,2}])^2 - 2*(1-v)*(D[Wxy,{x,2}]* D[Wxy,{y,2}]-(D[Wxy,x,y]^2)))
is 2 1/2 pages of expression and this
Expand[ ((D[Wxy,{x,2}]+D[Wxy,{y,2}])^2 - 2*(1-v)*(D[Wxy,{x,2}]* D[Wxy,{y,2}]-(D[Wxy,x,y]^2)))]
is about 40 pages of expression.

It is fortunate that in the Expanded version all the terms are fairly simple and have no denominators containing anything but small integer constants and Pi.

I had already waited a while and finally written "I suggest trying to Integrate the Expanded version and give it a day or three to see if you get an answer" when I was astonished to see:

In[8]:= Timing[U = (1/2)*d* Integrate[Expand[ ((D[Wxy,{x,2}] + D[Wxy,{y,2}])^2 - 2*(1-v)*(D[Wxy, {x, 2}]* D[Wxy,{y, 2}] - (D[Wxy,x,y]^2)))], {x, -a, a}, {y, 0, b}]]

Out[8]= {237.952*Second, (128*d*(739200*C3^2 + 335301120*C4^2 + 335301120*C4*C5 + 339440640*C4*C6 + 4139520*C5*C6 + 4139520*C6^2 + 242457600*C3*C7 + 1687910400*C7^2 + 2956800*C3*C8 + 1687910400*C7*C8 + 5913600*C3*C9 + 1708748800*C7*C9 + 20838400*C8*C9 + 20838400*C9^2 + 637560*C3^2*Pi^2 + 25138080*C4^2*Pi^2 + 4181760*C4*C5*Pi^2 + 5239080*C5^2*Pi^2 + 4646400*C4*C6*Pi^2 + 464640*C5*C6*Pi^2 + 2793120*C6^2*Pi^2 + 3801600*C3*C7*Pi^2 + 117152640*C7^2*Pi^2 + 380160*C3*C8*Pi^2 + 11658240*C7*C8*Pi^2 + 26373600*C8^2*Pi^2 + 4086720*C3*C9*Pi^2 + 12953600*C7*C9*Pi^2 + 1295360*C8*C9*Pi^2 + 13016960*C9^2*Pi^2 + 493020*C3^2*Pi^4 + 1880208*C4^2*Pi^4 + 3206016*C4*C5*Pi^4 + 1848528*C5^2*Pi^4 + 3237696*C4*C6*Pi^4 + 3206016*C5*C6*Pi^4 + 1880208*C6^2*Pi^4 + 2376000*C3*C7*Pi^4 + 8333760*C7^2*Pi^4 + 2344320*C3*C8*Pi^4 + 15152640*C7*C8*Pi^4 + 8276160*C8^2*Pi^4 + 2803680*C3*C9*Pi^4 + 15210240*C7*C9*Pi^4 + 15152640*C8*C9*Pi^4 + 8333760*C9^2*Pi^4 + 13365*C3^2*Pi^6 + 1980*C4^2*Pi^6 + 7920*C5^2*Pi^6 + 17820*C6^2*Pi^6 + 3600*C7^2*Pi^6 + 14400*C8^2*Pi^6 + 35640*C3*C9*Pi^6 + 32400*C9^2*Pi^6 + 2970*C2^2*Pi^2*(315 + 158*Pi^2 + 2*Pi^4) + 1485*C1^2*(40320 + 3864*Pi^2 + 332*Pi^4 + Pi^6) + 2640*C2*(1120*C9 + 2835*C8*Pi^2 + 144*C9*Pi^2 + 1038*C8*Pi^4 + 888*C9*Pi^4 + 6*C8*Pi^6 + 24*C7*(3780 + 54*Pi^2 + 37*Pi^4) + C3*(280 + 84*Pi^2 + 270*Pi^4)) + 1320*C1*(362880*C7 + 181440*C8 + 183680*C9 + 27864*C7*Pi^2 + 2592*C8*Pi^2 + 2880*C9*Pi^2 + 2124*C7*Pi^4 + 1776*C8*Pi^4 + 1800*C9*Pi^4 + 3*C7*Pi^6 + 108*C2*(420 + 14*Pi^2 + 5*Pi^4) + 2*C3*(22960 + 840*Pi^2 + 279*Pi^4))))/(155925*Pi^4)}

That is on a fairly old slow machine. You need to verify this for yourself.

My thinking is that Integrate might be faster on an integrand with very simple terms, in spite of having lots of them, than it is on products of powers of D[] that it might be evaluating repeatedly, although it isn't supposed to be doing that.

So try it with and without Expand. Throw a dozen minutes or an hour at each version and see if you get an answer both ways.

 

[phyzguy]

I also got it to evaluate by simplifying the terms first and then forcing it to integrate term by term. The notebook is attached. I think it may be the same result as Bill Simpson's. here's the final result:

1/(155925 \[Pi]^4)
  128 d (739200 C3^2 + 335301120 C4^2 + 335301120 C4 C5 + 
    339440640 C4 C6 + 4139520 C5 C6 + 4139520 C6^2 + 
    242457600 C3 C7 + 1687910400 C7^2 + 2956800 C3 C8 + 
    1687910400 C7 C8 + 5913600 C3 C9 + 1708748800 C7 C9 + 
    20838400 C8 C9 + 20838400 C9^2 + 637560 C3^2 \[Pi]^2 + 
    25138080 C4^2 \[Pi]^2 + 4181760 C4 C5 \[Pi]^2 + 
    5239080 C5^2 \[Pi]^2 + 4646400 C4 C6 \[Pi]^2 + 
    464640 C5 C6 \[Pi]^2 + 2793120 C6^2 \[Pi]^2 + 
    3801600 C3 C7 \[Pi]^2 + 117152640 C7^2 \[Pi]^2 + 
    380160 C3 C8 \[Pi]^2 + 11658240 C7 C8 \[Pi]^2 + 
    26373600 C8^2 \[Pi]^2 + 4086720 C3 C9 \[Pi]^2 + 
    12953600 C7 C9 \[Pi]^2 + 1295360 C8 C9 \[Pi]^2 + 
    13016960 C9^2 \[Pi]^2 + 493020 C3^2 \[Pi]^4 + 
    1880208 C4^2 \[Pi]^4 + 3206016 C4 C5 \[Pi]^4 + 
    1848528 C5^2 \[Pi]^4 + 3237696 C4 C6 \[Pi]^4 + 
    3206016 C5 C6 \[Pi]^4 + 1880208 C6^2 \[Pi]^4 + 
    2376000 C3 C7 \[Pi]^4 + 8333760 C7^2 \[Pi]^4 + 
    2344320 C3 C8 \[Pi]^4 + 15152640 C7 C8 \[Pi]^4 + 
    8276160 C8^2 \[Pi]^4 + 2803680 C3 C9 \[Pi]^4 + 
    15210240 C7 C9 \[Pi]^4 + 15152640 C8 C9 \[Pi]^4 + 
    8333760 C9^2 \[Pi]^4 + 13365 C3^2 \[Pi]^6 + 1980 C4^2 \[Pi]^6 + 
    7920 C5^2 \[Pi]^6 + 17820 C6^2 \[Pi]^6 + 3600 C7^2 \[Pi]^6 + 
    14400 C8^2 \[Pi]^6 + 35640 C3 C9 \[Pi]^6 + 32400 C9^2 \[Pi]^6 + 
    2970 C2^2 \[Pi]^2 (315 + 158 \[Pi]^2 + 2 \[Pi]^4) + 
    1485 C1^2 (40320 + 3864 \[Pi]^2 + 332 \[Pi]^4 + \[Pi]^6) + 
    2640 C2 (1120 C9 + 2835 C8 \[Pi]^2 + 144 C9 \[Pi]^2 + 
       1038 C8 \[Pi]^4 + 888 C9 \[Pi]^4 + 6 C8 \[Pi]^6 + 
       24 C7 (3780 + 54 \[Pi]^2 + 37 \[Pi]^4) + 
       C3 (280 + 84 \[Pi]^2 + 270 \[Pi]^4)) + 
    1320 C1 (362880 C7 + 181440 C8 + 183680 C9 + 27864 C7 \[Pi]^2 + 
       2592 C8 \[Pi]^2 + 2880 C9 \[Pi]^2 + 2124 C7 \[Pi]^4 + 
       1776 C8 \[Pi]^4 + 1800 C9 \[Pi]^4 + 3 C7 \[Pi]^6 + 
       108 C2 (420 + 14 \[Pi]^2 + 5 \[Pi]^4) + 
       2 C3 (22960 + 840 \[Pi]^2 + 279 \[Pi]^4)))