sparkle123
- 172
- 0
Figure 14-24 shows a tank filled with water. Five horizontal floors and ceilings are indicated;
all have the same area and are located at distances L, 2L, or 3L below the top of the tank. Rank them according to the force on them due to the water, greatest first.
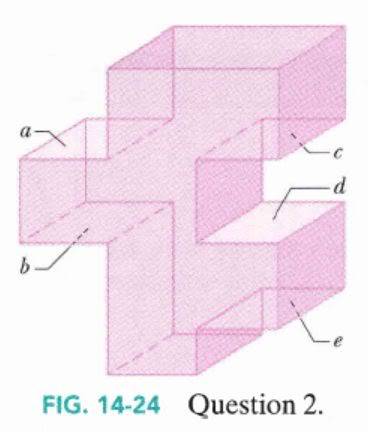
Are we just comparing the heights?
So e>b=d>a=c?
Thanks!
all have the same area and are located at distances L, 2L, or 3L below the top of the tank. Rank them according to the force on them due to the water, greatest first.
Are we just comparing the heights?
So e>b=d>a=c?
Thanks!