Wave equation for an elastic rod

[thomas19981]

1. Homework Statement
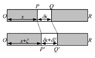
The figure below shows a section of a thin, elastic rod of density $\rho$, cross sectional area $A$, and modulus of elasticity $E$.

By considering the net force acting on an element of the rod, derive the wave equation governing its longitudinal motion:

$\frac{\partial^2(\xi)}{\partial t^2}=\frac{E}{\rho}\frac{\partial^2(\xi)}{\partial x^2}$

where $\xi$ is the displacement of the medium from its equilibrium position.

Homework Equations

The Attempt at a Solution

My solution is inserted as an image but I can't see where I'm going wrong with this question.
Many thanks in advance.

 

[Orodruin]

You are missing the fact that there are two forces acting on each element of the rod. One to the left and one to the right. Both are proportional to the strain at their respective locations.

 

[thomas19981]

You are missing the fact that there are two forces acting on each element of the rod. One to the left and one to the right. Both are proportional to the strain at their respective locations.

You are missing the fact that there are two forces acting on each element of the rod. One to the left and one to the right. Both are proportional to the strain at their respective locations.

Hi. I've considedered the two forces in the different locations but I seem to be running into a similar problem.

 

[Orodruin]

Can you please write down your work in text rather than attaching it as images? (As stated in the homework rules.) It is very annoying to have to look at a computer screen turned 90 degrees and to read your hand-written things in relatively bad resolution.