NYROCKFAN
- 34
- 0
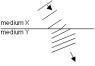
In the diagram shown:
All points on anyone wave front shown must be:
a) traveling with the same speed
b) traveling in the same medium
c) in phase
d) superposed
We never did wave fronts in class, and this is a question on my graded review packet for our final. I think the answer is d, am I correct? I'm pretty sure it's not a or b, because the waves would be changing speed and medium.
All points on anyone wave front shown must be:
a) traveling with the same speed
b) traveling in the same medium
c) in phase
d) superposed
We never did wave fronts in class, and this is a question on my graded review packet for our final. I think the answer is d, am I correct? I'm pretty sure it's not a or b, because the waves would be changing speed and medium.