SUMMARY
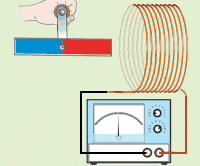
The discussion centers on the graphical representation of the electromotive force (emf) induced in a coil by a bar magnet spinning perpendicular to the coil's axis. Participants agree that the induced waveform resembles a sine wave, characterized by alternating double positive and negative peaks due to the rotation of the magnet's North and South poles. The voltage generated is proportional to the rate of change of magnetic flux through the coil, with specific parameters such as the length and diameter of the coil and the distance from the coil to the magnet being crucial for accurate representation. The complexity of the phenomenon is acknowledged, with references to Faraday's law and the need for precise geometric definitions.
PREREQUISITES
- Understanding of Faraday's law of electromagnetic induction
- Knowledge of sine wave characteristics and waveform analysis
- Familiarity with magnetic flux concepts and their relation to coil geometry
- Basic principles of electromagnetism and magnetic field behavior
NEXT STEPS
- Research "Faraday's law of electromagnetic induction" for foundational understanding
- Explore "sine wave generation in electromagnetic systems" for waveform analysis techniques
- Study "magnetic flux calculations in coils" to understand the impact of geometry on induced emf
- Investigate "electromagnetic field theory" to deepen knowledge of magnetic field interactions
USEFUL FOR
Physics students, electrical engineers, and anyone interested in the principles of electromagnetic induction and waveform analysis in coil systems.