- #1
greggory
- 14
- 0
"Waves" of sine expression
So, I have been working with a lot of Math today(sorry if I am asking so many questions), and I found and expression. All sine functions use radians.
sin(y) + sin(y) / sin(y)
Now, assuming you start with 1, if you were to plot y on a graph with variable x increasing each time calculated, you would get something like this:
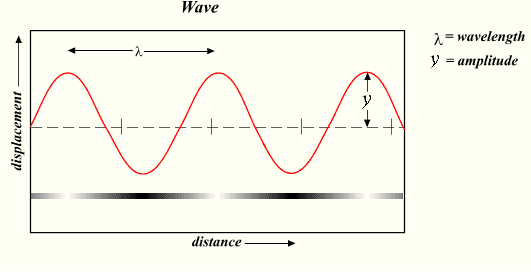
This image isn't mine, so this is just something identicle.
Can this be explained?
So, I have been working with a lot of Math today(sorry if I am asking so many questions), and I found and expression. All sine functions use radians.
sin(y) + sin(y) / sin(y)
Now, assuming you start with 1, if you were to plot y on a graph with variable x increasing each time calculated, you would get something like this:
This image isn't mine, so this is just something identicle.
Can this be explained?