Weight distribution on both ends of a ramp?

[jbriggs444]

I offer this drawing that conforms to a simple beam setup with purely vertical support forces on a beam between two scales at different heights. The beam is at angle $\theta$ from the horizontal.

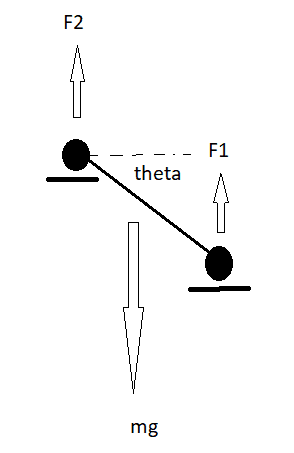
Case 1: I claim that the beam can be in equilibrium with both $F_1$ and $F_2$ purely vertical. In this case, both support forces will have magnitude $\frac{mg}{2}$

Case 2: I claim that an alternate possibility is for $F_2$ to be changed to a diagonal direction, up and to the right. If this is done, $F_1$ must also be changed to a non-vertical direction, likely up and to the left. We might then ask:

"If we fix the bottom end in place with a hinge, what is the minimum magnitude for force $F_2$ that can hold the beam in place? At what angle from the horizontal would $F_2$ then be exerted?

Case 3: I claim that is another possibility. $F_1$ could be changed to a diagonal direction, up and to the right. If this is done, $F_2$ must be changed. This time to a direction that is likely up and to the left. We can again ask a question:

"If we fix the top of the beam in place with a hinge, what is the minimum magnitude for force $F_1$ that can hold the beam in place? At what angle from the horizontal would $F_1$ then be exerted?

Roughly speaking, case 1 corresponds to a toy wagon sitting on a flight of stairs.
Roughly speaking, case 2 corresponds to a roofer pushing a ladder away from the eaves.
Roughly speaking, case 3 corresponds to a person holding a pendulum at an angle.

 

[dcb]

As berkeman pointed out to me, I have morphed the discussion into something different than the original post so I apologize but I was interested xshovelfighter's observation of inclined push up's and carrying a couch.

If you assume the couch has zero height everything you say is correct. The height of the couch changes it's center of gravity as the stair angle increases so it is important to the discussion.Couch Problem

Above is a link to a high resolution jpeg if you can't see my image.

The presumption is that the top & bottom guys grasp the bottom of the couch along it's base and let their arms hang down to support it's weight. L is the length of the couch H is it's height and W it's weight.

Setting the bottom guy (B is his upward force) as the reference, W as the weight at the CG of the couch, and T is the upward force supplied by the top guy then
the horizontal moment arms are:

distance BT = L*cos(theta)
distance BW = L/2*cos(theta) - H/2*sin(theta)
Note this cause the CG of the couch to move back more quickly than the base of the couch. Setting H to 0 causes the B and T forces to be W/2 for all angles.

sum of horizontal moment arms around B=0=T*BT-W*BW thus T=W*BW/BT
sum of the Y forces = 0 = W-T-B thus B=W-T

setting L=7, H=2, W=200# and theta=45 degrees

T=72# , B=128#

Somewhere around theta=74 degrees T=0 and B=W=200# so the top guy is doing nothing.

At 75 degrees the CG goes over the top of the bottom guy and flips over unless the top guy has arms long enough to pull the couch back.

The bottom guy has to adjust his grip to the center of the side of the couch (H/2) to keep the CG from flipping the couch.

Does this make sense?

 

[dcb]

This approximates what I see on a scale when I put one end of dumbbell on it and slowly lift the other end.

 

[jbriggs444]

Somewhere around theta=74 degrees T=0 and B=W=200# so the top guy is doing nothing.

I agree with pretty much everything you are pointing out about a couch with non-zero height. However, I want to explore the situation here with $\theta = 74$ degrees. This is a couch with length 7 and height 2.

At 74 degrees, I expect that it can balance on its lower left corner. But let us check that assertion...$$74 \text{ degrees} = arctan(7/2)$$Yes. It is balanced on the lower left corner.

The bottom guy is supporting the couch at its lower left corner. This is at the balance point. The upper guy is supporting the couch at its upper right corner. This is not at the balance point.

Yes, I agree that in this scenario, if both guys are supporting the couch with purely vertical forces, the bottom guy must support the full weight. The top guy can support nothing.

Of course, if the two fellows were holding the couch from the upper left and upper right corners, the situation would be reversed. The top guy would have to supply all of the supporting force and the bottom guy could supply nothing. The couch would be hanging, balanced, from the top guy's hands (in an incredibly difficult posture).

This approximates what I see on a scale when I put one end of dumbbell on it and slowly lift the other end.

Edit: Some reprasing below as I had lost track of which end of the dumbbell was on the scale.

I claim that this is not a well defined experimental procedure. What horizontal force are you exerting on the scale with your hand as the dumbell pivots about its opposite end the end on the scale?

If the horizontal force is zero, then the vertical support force will be split 50/50 regardless of the tilt angle all the way up to just short of a purely vertical dumbbell.

Of course, you may have difficulty applying a purely vertical force with a platform scale your hand as the dumbbell approaches the vertical. You may have to switch to a cord and a tension based force measurement device and arrange carefully for the cord to remain vertical. If this is done, the situation when the dumbbell is purely vertical is statically indeterminate. This was pointed out in post #3 back in 2016:

PS This is true for all angles except absolutely vertical. In that position you cannot determine which end carries what percentage of the weight. It's said to be statically indeterminate.

 

[dcb]

Thank you for joining in this discussion. Every time I try to figure out the X forces it makes no sense to me.

I think that if both guys could somehow grab their end of the couch at h/2 instead of the base, everything changes.

I'm out of the country in a few days for the month of April so I'd like to pick up the discussion then.

 

[dcb]

I now understand your argument about the scale. It seemed to me like the scale is designed to only measure Y forces but I got inconsistent results in an experiment. Intuitively it seems like the X forces are 0 at 0 degrees reach a maximum at 45 and go back to 0 at 90 (at least for H=0).

I grabbed a 2x8 sitting around in the garage and a device measures angles by using gravity to point a needle straight up. I put double sided tape on the scale so the 2x8 wouldn't slip. The 2x8 had some knots in it so the weight distribution was likely not perfectly uniform.

So as to not bias the experiment I did the scale measurements first. I measured the bottom left edge of the 2x8 at 20 degrees and 45 degrees and got 785 grams and 1160 grams. I used my finger at the bottom right edge to push it up. I pretty much kept the force on my finger perpendicular to the H edge.

I then measured the length to be 452 mm and the height to be 184 mm and the board weighed 1368 grams.

When I did the math I got 787 grams at 20 degrees which is pretty close. At 45 degrees I got 962 grams so the scale is measuring some X force at least at the worst angle.

When I get time I'll build form a nail out of some tubular metal at the right height for 45 degrees (plus the scale height), put it under the right edge and redo the experiment.

 

[jbriggs444]

I pretty much kept the force on my finger perpendicular to the H edge.

Yes, this is important.

I assumed a vertical support force on both ends -- that being the relevant case for a buoy supporting one end of a dock. You are assuming a perpendicular support force at the free end with a hinge joint (e.g. tape) at the scale end.

In your scenario there is nothing indeterminate. We can solve for the support forces and their angles at both ends as a function of the beam angle. There are no angles for which a solution is unavailable.

We begin by labelling the forces and endpoints. We have a beam with one end free and the other end hinged to the floor. Let us arbitrarily say that it is the left end that is hinged. Call this point "L". The right end is free. Call it "R".

We can imagine that "L" is at the origin of our coordinate system. The beam is making some angle $\theta$ that probably lies in the first quadrant. (The analysis also works for the 2nd, 3rd or 4th quadrants).

The beam has mass $m$ and length $l$.

We want to solve for unknown forces $F_\text{Lx}$ and $F_\text{Ly}$ for the horizontal and vertical components of the support force from hinge on beam at point L and for the unknown force $F_\text{Rt}$ for tangential component of the force of your hand on the beam at point R.

We are assuming that the radial component of the force of your hand on the beam is zero.

We can begin with a torque balance, summing torques about the hinge at point L. The result should be a zero if you are exerting just enough force to hold the beam in place having lifted it.

There are only two forces on the beam that have lines of action that do not pass through the chosen axis. One is gravity ($\vec{mg}$). The other is the tangential force from your hand, $F_\text{Rt}$. The moment arm for gravity has length $\frac{l}{2}$. But that moment arm may not be perpendicular to the force. So we have to multiply by $\cos \theta$. The moment arm for the tangential force for your hand is $l$. That moment arm is perpendicular already. Gravity acts clockwise. Your hands act counterclockwise.

Put it together and we have:$$0 = \frac{1}{2} mgl \cos \theta - F_\text{Rt}l$$We want to solve this for $F_\text{Rt}$. That easy -- we just divide both sides by $l$ and add $F_\text{Rt}$ to both sides:$$F_\text{Rt} = \frac{1}{2}mg \cos \theta$$But this is not the only number we care about.

Let us now do a force balance in the $y$ direction, summing the vertical components of all forces acting on the beam. There are three such forces, $F_\text{Ly}$ from the hinge, $mg$ from gravity and the $y$ component of $F_\text{Rt}$ from your hand. That $y$ component will be given by $F_\text{Rt} \cos \theta$. Put it togther and substitute in our solution for $F_\text{Rt}$ above and we get:$$0 = F_\text{Ly} - mg + \frac{1}{2} mg \cos^2 \theta$$We can move the terms around and arrive at:$$F_\text{Ly} = mg (1 - \frac{1}{2} \cos^2 \theta)$$Then we can apply a trig identity: $2 cos^2 \theta - 1 =\cos 2 \theta$ (or, equivalently $\cos^2 \theta\ = \frac{\cos 2 \theta + 1}{2}$) to arrive at:$$F_\text{Ly} = mg \frac{3 - cos 2 \theta}{4}$$That was a bit more algebraic manipulation than I can usually complete correctly, so a quick sanity check is in order.

For $\theta$ = 0, the result is $\frac{mg}{2}$ as expected.
For $\theta$ = 90, the result is $mg$ as expected
For $\theta$ = -90, the result is $mg$ as expected.

Let us finish with a force balance in the $x$ direction, summing the horizontal components of all forces acting on the beam. There are two such forces, $F_\text{Lx}$ from the hinge and the $x$ component of $F_\text{Rt}$ from your hand. That $x$ component will be given by $-F_\text{Rt} \sin \theta$. Put it together and we have:$$F_\text{Lx} = \frac{1}{2}mg \sin \theta \cos \theta$$We can simplify this using the double angle formula for the sine function: $\sin 2 \theta = 2 \sin \theta \cos \theta$ (or $\frac{1}{2} \sin \theta \cos \theta = \frac{\sin 2 \theta}{4}$). This will yield:
$$F_\text{Lx} = \frac {mg \sin 2 \theta} {4}$$For $\theta$ = 0, the result is 0 as expected.
For $\theta$ = 45, the result is maximized at $\frac{mg}{4}$
For $\theta$ = 90, the result is back to 0 as expected.

Your result that the x component of the tangential force is maximized at 45 degrees is confirmed.

Intuitively it seems like the X forces are 0 at 0 degrees reach a maximum at 45 and go back to 0 at 90 (at least for H=0).

Edit: Fixed the sign convention on the $x$ components to right = positive.