lelandsthename
- 12
- 0
What am I doing wrong?? - Linear Differential Equations
Hi everyone, the problem I have is listed under my attempt (I hope it's ok that I pasted it): to solve the below linear differential equation with the initial condition y(1)=1
P(x) and Q(x) linear differential equation solution method
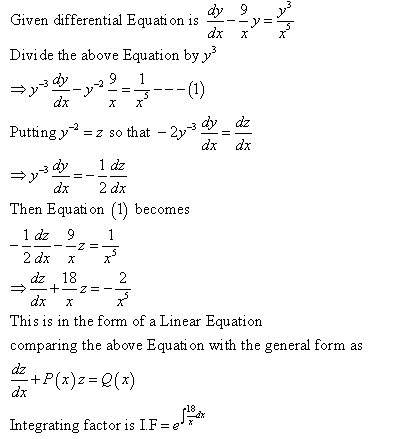
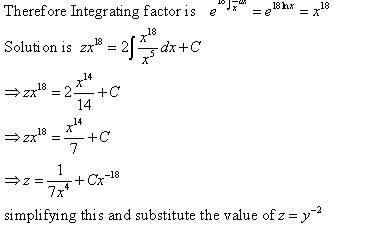
Plugging in for 1=y and 1=x to solve for c has yielded me crazy results after i plugged in y^(-2). I got both c=6/7 and c=-1/6 but neither are the correct answer (this problem is listed on a program that allows me to check my answer) can anyone help me explain if I did a step wrong or if I am solving for C wrong??
Thanks!
Homework Statement
Hi everyone, the problem I have is listed under my attempt (I hope it's ok that I pasted it): to solve the below linear differential equation with the initial condition y(1)=1
Homework Equations
P(x) and Q(x) linear differential equation solution method
The Attempt at a Solution
Plugging in for 1=y and 1=x to solve for c has yielded me crazy results after i plugged in y^(-2). I got both c=6/7 and c=-1/6 but neither are the correct answer (this problem is listed on a program that allows me to check my answer) can anyone help me explain if I did a step wrong or if I am solving for C wrong??
Thanks!
Last edited: