Clari
- 62
- 0
hi there,
i have two questions concerning operational amplifier which i can't figure out. i have tried them for hours, and finally get on a bit, yet i am not sure whether i have the answer right. :(
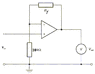
1a. What is the value of the feedback resistance in figure 1?
My ans: V_out/ V_in = 1+ R_f/ R_in
30/ 6 = 1+ R_f/ 10 x 10^3
R_f = 40000 ohm
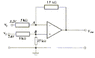
2. In figure 2, Assume the op amp does not saturate, find the potentials at A and B.
At A, the current = 3.2 x 5k = 0.64 mA
At B, the current = 2.8 x (5k+15K) = 0.14 mA
Total current = 0.64 + 0.14 = 0.78 mA
Potential at A = (0.78 -0.64) x 15k = 2.1V
Potential at B = 0.14mA x 15k = 2.1V
please help me. ^^
i have two questions concerning operational amplifier which i can't figure out. i have tried them for hours, and finally get on a bit, yet i am not sure whether i have the answer right. :(
1a. What is the value of the feedback resistance in figure 1?
My ans: V_out/ V_in = 1+ R_f/ R_in
30/ 6 = 1+ R_f/ 10 x 10^3
R_f = 40000 ohm
2. In figure 2, Assume the op amp does not saturate, find the potentials at A and B.
At A, the current = 3.2 x 5k = 0.64 mA
At B, the current = 2.8 x (5k+15K) = 0.14 mA
Total current = 0.64 + 0.14 = 0.78 mA
Potential at A = (0.78 -0.64) x 15k = 2.1V
Potential at B = 0.14mA x 15k = 2.1V
please help me. ^^
 well, i have also tried the alternative method before but i don't know why the two voltages have to subtracted from each other.
well, i have also tried the alternative method before but i don't know why the two voltages have to subtracted from each other.