What are the components and sum of two vectors?

[physicsss]

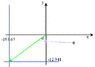
Vector V1 is 7.59 units long and points along the negative x axis. Vector V2 is 4.34 units long and points at +55.0° to the positive x axis.

(a) What are the x and y components of each vector?
I got:
V1x = -7.59
V1y = 0
V2x = 2.49
V2y = 3.56

(b) Determine the sum V1 + V2 (magnitude and angle).
I got:
6.22

All of the above is correct when I submitted it, but the angle was wrong. I've tried entering -34.9 and 34.9, but they are all wrong. Any ideas?

 

[HallsofIvy]

Gosh, I hate these "submit to a computer" things! So often they are "wrong" just because you have too many significant figures or some picky thing like that.

But in this case, you answer is simply "completely" wrong.

The problem is that arctan, like all of the inverse trig functions is "multi-valued"
Adding the two vectors in component form, you get <-4.8,3.56> and the angle is given by arctan(-3.56/4.8)= arctan(-.742). You calculator can only give one answer and so gives the "principal" value, -36.6 degrees.
Since we are measuring angles from the positive x-axis, that would correspond to a vector pointing down and to the right: <4.8,-3.56> (Obviously, the arctan has no way of "knowing" if the negative is from the numerator or denominator).
But the correct vector is <-4.8, 3.56> which points up and to the right: you need to add 180 degrees. The correct angle is 180- 36.6= 143.4 degrees.

 

[physicsss]

How did you get -4.8?

 

[physicsss]

What would the angle be if the x-component is -193.65 and the y-component is -12.941? anyone?

 

[Leong]

What would the angle be if the x-component is -193.65 and the y-component is -12.941? anyone?

tan\theta=\frac{193.65}{12.941}
\theta=86.177^0
don't insert the negative sign, just treat it as a normal triangle with certain lengths which are always positive.
so, you can say that the vector makes an angle of –(90+86.177)=-176.177 degree from the positive x-axis; or
(360-176.177)=183.823 degree from the positive x-axis.

 

[HallsofIvy]

How did you get -4.8?

By adding, just as the problem said to do:
(-7.59, 0)+ (2.49, 3.56)= (-7.59+ 2.49, 0+ 3.56)= (-5.1, 3.56)

Hmm, blasted calculator doesn't know what it's doing!

 

[HallsofIvy]

tan\theta=\frac{193.65}{12.941}
\theta=86.177^0
don't insert the negative sign, just treat it as a normal triangle with certain lengths which are always positive.
so, you can say that the vector makes an angle of –(90+86.177)=-176.177 degree from the positive x-axis; or
(360-176.177)=183.823 degree from the positive x-axis.

OR put in the negative sign: tan\theta= \frac{-193.65}{-12.941} and then observe that the negatives cancel!

 

[physicsss]

Um...tan x=y/x...should it be tan^-1(12.941/193.65)?

 

[Leong]

There are two ways to find the angle:
1. Draw the vector, find the angle you want by treating it like a right triangle using trig like what i have done.
2. Use the vector notation, \vec{a}= x\vec{i} + y\vec{j}
Then, tan\ \theta = \frac{y}{x}

I use option #2 here.

\vec{a}=-193.65\vec{i}-12.941\vec{j}
tan\ \theta = \frac{-12.941}{-193.65}
Your calculator will give \theta=3.8232^0
See HallofIvy's point in post #2?
Your calculator will give the principal value to you.
But you know that \vec{a} lies in the 3rd quadrant. so you should add 180 degree to the answer you have just got; i.e. 183.82 degree; just like what we have got using option #1 method.

and when you use the formula to find the angle by method #2. the angle is always relative to the positive x-axis.find the principal value, identify the quadrant where the vector lies. add some appropriate degree and get the answer.

 

[cdhotfire]

arent vectors fun , hehe.