What Are the Components of Net Force for a Mass Swinging on a Rope?

Click For Summary
SUMMARY

The discussion centers on analyzing the components of net force for a 2 kg mass swinging on a rope at a 56-degree angle to the horizontal. The tension in the rope is given as 16.25 N, while the gravitational force acting on the mass is calculated to be -19.6 N. The user struggles with vector addition and the correct direction of the forces involved, indicating a need for clarity on vector components and their magnitudes in this context.

PREREQUISITES
  • Understanding of vector components in physics
  • Knowledge of gravitational force calculations
  • Familiarity with trigonometric functions and their application in physics
  • Basic principles of tension in a swinging mass system
NEXT STEPS
  • Study vector addition and decomposition of forces in physics
  • Learn about the role of tension and gravity in circular motion
  • Explore trigonometric functions, specifically sine and cosine, in force calculations
  • Review examples of forces acting on objects in motion, particularly in pendulum scenarios
USEFUL FOR

This discussion is beneficial for physics students, educators, and anyone interested in understanding the dynamics of forces acting on objects in motion, particularly in pendulum-like systems.

cfagan6
Messages
1
Reaction score
0

Homework Statement


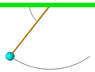
2 kg mass swings on the end of a rope as shown in the figure below. At the highest point in the trajectory the string makes a 56 degree angle with respect to the horizontal and the tension on the string is 16.25 N.

= (No Response) N

Homework Equations


So I know I need to the direction of Ft and Fg.
Ft^hat=<cos(56),sin(56),0>
Fgrav^hat=<cos(56),sin(56),0>
Ft=16.25
Fgrav=-19.6

The Attempt at a Solution


So I'm not quite sure what to do now. The way I tried doing it was adding the two vectors times their magnitudes and finding the magnitude of that vector but I get the wrong answer. I feel that the problem is in directions of my forces but I don't understand why.
 

Attachments

  • pendulum10.png
    pendulum10.png
    1.1 KB · Views: 588
Physics news on Phys.org
What is the question? ehild
 

Similar threads

Net force and position of objects in space
  • · Replies 2 ·
Replies
2
Views
2K
How is centripetal force involved here? (charged mass sliding down a conducting hemisphere)
  • · Replies 31 ·
2
Replies
31
Views
2K
Direction of the net force acting on a pendulum
  • · Replies 10 ·
Replies
10
Views
3K
Determine the speed and tension of keys swinging in a circular path
  • · Replies 8 ·
Replies
8
Views
2K
Confusion with force components
  • · Replies 21 ·
Replies
21
Views
3K
Magnitude of net Gravitational Force
  • · Replies 1 ·
Replies
1
Views
5K
Calculating Net Force of Particle 5: A Problem Overview
  • · Replies 7 ·
Replies
7
Views
2K
Finding the position of a middle charge to have Zero Net Force
  • · Replies 9 ·
Replies
9
Views
3K
Vector is a function of its position or not?
  • · Replies 16 ·
Replies
16
Views
2K
Calculate the net force acting on the object
  • · Replies 5 ·
Replies
5
Views
3K