What are the dimensions of the shapes in this tangram problem?

[narledge]

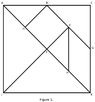
I am currently working on an assignment using Tanagrams. I have the information that I have:
• 2 large, and congruent, isosceles right triangles
• 1 medium isosceles right triangle
• 2 small, and congruent, isosceles right triangles
• 1 square
• 1 parallelogram

The pieces can be rearranged with no gaps or overlapping of shapes into a square with dimensions 1 unit by 1 unit (i.e., the entire area of the square is 1 unit^{2})

You must find the dimensions of all shapes and cannot make midpoint assumptions.

Each dimension must be supported by geometric justification. I have attached a picture and would appreciate any help in reaching an answer.View attachment 5180

View attachment 5181

 

[MarkFL]

Hello and welcome to MHB, narledge! :D

We ask that our users show their progress (work thus far or thoughts on how to begin) when posting questions. This way our helpers can see where you are stuck or may be going astray and will be able to post the best help possible without potentially making a suggestion which you have already tried, which would waste your time and that of the helper.

Can you post what you have done so far?

 

[narledge]

I am sorry for not doing that ----

I have found the length of AB, AF, FK, and FJ by using the given dimensions of 1 and Pythagorean theorem.

The sides of the smaller two triangles at 1/2 for hypotenuse and square root of 2 /4

The sides of the medium are hypotenuse square root of 2/2 and side 1/2

square is side square root of 2/4

parallelogram sides square root of 2/4 and 1/2

Just having difficulty proving it using geometry.

 

[MarkFL]

Okay, we are given:

$$\overline{AJ}=\overline{JK}=1$$

And since $$\triangle AFJ$$ and $$\triangle JFK$$ are right isosceles triangles, we know by Pythagoras:

$$\overline{AF}=\overline{JF}=\overline{FK}=\frac{\sqrt{2}}{2}$$

From this, we may conclude that $F$ is at the mid-point of the square $AJKC$. Can you justify that $\overline{BF}$ has to be a vertical line, and thus $$\overline{AB}=\overline{BC}=\frac{1}{2}$$?