narledge
- 4
- 0
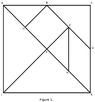
I am currently working on an assignment using Tanagrams. I have the information that I have:
• 2 large, and congruent, isosceles right triangles
• 1 medium isosceles right triangle
• 2 small, and congruent, isosceles right triangles
• 1 square
• 1 parallelogram
The pieces can be rearranged with no gaps or overlapping of shapes into a square with dimensions 1 unit by 1 unit (i.e., the entire area of the square is 1 unit^{2})
You must find the dimensions of all shapes and cannot make midpoint assumptions.
Each dimension must be supported by geometric justification. I have attached a picture and would appreciate any help in reaching an answer.View attachment 5180
View attachment 5181
• 2 large, and congruent, isosceles right triangles
• 1 medium isosceles right triangle
• 2 small, and congruent, isosceles right triangles
• 1 square
• 1 parallelogram
The pieces can be rearranged with no gaps or overlapping of shapes into a square with dimensions 1 unit by 1 unit (i.e., the entire area of the square is 1 unit^{2})
You must find the dimensions of all shapes and cannot make midpoint assumptions.
Each dimension must be supported by geometric justification. I have attached a picture and would appreciate any help in reaching an answer.View attachment 5180
View attachment 5181