What Are the Forces in Truss Members BH and HG?

[sophiebeth100]

Homework Statement

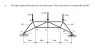
The right triangles of the plane truss are all the same. What are the forces in members BH and HG?

Diagram for question is below, or a link:
http://puu.sh/nsw1k/aad8a8b134.png

Homework Equations

n/a

The Attempt at a Solution

Reaction force at A + reaction force at E are equal, therefore both = 15kN.

It was after this point I became stuck.

I calculated the forces in the x axis:
ABcos60 + AHcos30 = 0
Then in the y axis:
ABcos30 + AHcos30 = 15kN

Not sure if the above is correct, and not sure how to continue with the question. Any help would be great!

 

[haruspex]

You can get more equations by considering the balance of forces at each node. But that could generate a lot of equations and a lot of unknowns.
Using the symmetry, there are 7 unknowns.
It will help if you can find an easy one to start with. I suggest G. What do you notice there?

 

[sophiebeth100]

You can get more equations by considering the balance of forces at each node. But that could generate a lot of equations and a lot of unknowns.
Using the symmetry, there are 7 unknowns.
It will help if you can find an easy one to start with. I suggest G. What do you notice there?

Perhaps that GC is equal to 12kN? Not entirely sure if that's right but if so I could work from there.

 

[haruspex]

Perhaps that GC is equal to 12kN? Not entirely sure if that's right but if so I could work from there.

No, that isn't right.
What forces act at G? What are their directions?

 

[sophiebeth100]

No, that isn't right.
What forces act at G? What are their directions?

I wouldn't think there are any forces in the x-axis since the total force in the x-axis is zero.

Does the force at GC act upwards? Equal to the total downward force, so 30kN?

 

[haruspex]

I wouldn't think there are any forces in the x-axis since the total force in the x-axis is zero.

Does the force at GC act upwards? Equal to the total downward force, so 30kN?

In analysing forces in such interconnected systems, you need to focus on one node at a time, just thinking about what that node experiences directly. The only forces node G feels are from the three members that meet there, it doesn't 'know' anything about the externally applied loads. (Only nodes B, C, D feel those.)
The forces from the three members meeting at G must balance both vertically and horizontally. That allows you to write two equations involving the forces in those members. What equations do you get?