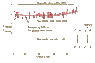I will try to construct a logical progression which is not necessarily historical. First SU(3) is suggested by the observed spectra of mesons and baryons, as multiplets of "constituent quarks". This is mostly quantum numbers, so we do not really address yet whether those are "naked" (current) or "dressed" (effective constituents). In particular, anytime we will start to "dress" a "naked" parton into a constituent, the process of doing so will always respect color SU(3) invariance which is not anomalous.
But constituent quark models predict in particular baryonic resonances which as of today are still missing. It is possible that extracting them from the cross sections requires extensive detailed analysis of multidimensional final states, taking into account properly various overlap (interferences) between broad states. It is also possible that those missing states simply do not exist, if for instance the naive constituent quark models do not use the right representations. Maybe baryons are constructed out of (quantum superpositions of) diquarks and quarks. So I will not go further in this direction, and indeed we have other evidence for SU(3).
Indirect and direct evidence can be obtained from electron positron annihilation. The earliest evidence (IIRC) comes from the ratio of the total annihilation cross section in hadrons compared to muons, and I think this is what you refer to. The ratio displays constant values as a function of center of mass energy, jumping to higher values as more quark flavors are involved. For
instance
See the full plots in figures
40.6 and 40.7
Further evidence can be obtained from scaling violation, comparing quark and gluon jets, their distributions in transverse momenta and other variables, all those evolving with the renormalization scale. I would rather not go into the details, many details. Essentially, the Lie algebra for SU(3) basically has "charges" in the fundamental and adjoint representations, to which respectively belong quarks and gluons, the ratio of those charges is characteristic of SU(3) and should be C_{A}/C_{F}=9/4.
These methods are sometimes described as "QCD radiophysics", as coherent soft gluon radiation amounts to antenna patterns.
Please find details in
The Scale Dependence of the Hadron Multiplicity in Quark and Gluon Jets and a Precise Determination of C_{A}/C_{F}
The final result quoted in the above paper is
C_{A}/C_{F}= 2.246 \,\, \pm 0.062_\text{(stat.)} \pm 0.080_\text{(syst.)} \pm 0.095_\text{(theo.)}
At this point, we may pause a little while. All of the above would still hold even if the SU(3) color would be approximate, in the sense that it would be slightly broken by a tiny gluon mass. "Tiny" must be compared to the typical hadronic scale, in between the pion and proton mass say. So 1 MeV is small and can easily hide. The data above is obtained at large energies. Electron positron annihilation does all sorts of nasty stuff around the GeV scale, due to contributions from various resonances of various width, as you can see in
40.6. People investigating the non-perturbative dynamics of cold hadrons do not have much luxury of using naked (perturbative) partons. We sort of circle back to the old constituent quarks, albeit with much more developed tools today. For instance
Bethe-Salpeter and Dyson-Schwinger methods give results in agreement with lattice QCD (when they can be compared). So I meant to say, we are doomed if we look for better limits on the gluon mass : high energy data does not help, because perturbative gluons are so relativistic, for all purpose they would look massless anyway. And low energy data does not help either, because gluons dress and do acquire a (gauge covariant) mass which is also large compared to the MeV limit Yndurain already published in 1995. The reference comes from particle data group :
"Limits on the gluon mass", Phys Let B 345 (1995) 524-526
The argument presented by Yundurain is a little bit more elaborated, but can be summarized as follow. It the gluon (at least one of them) has a small mass, the effective potential felt by a static quark pulled out from a hadron in which remains a diquark has a form Coulomb at short distance, linear at intermediate distances, and falls to zero from a Yukawa-type behavior -(constant) exp(r*m)/r at large distances. After some hand waving, Yndurain eventually uses a simple triangular potential, growing linearly from 0 to a critical fixed energy at a distance equal to the inverse gluon mass, and then dropping to zero. If the slope of the linear part is K, then the critical energy is K/m. The hand waving is supposedly justified by worse uncertainties.
Below the inverse gluon mass distance, quarks are attracted, but above this distance they are repelled. From the non-observation of free quarks produced in high energy collisions, he concludes a bound on the gluon mass of the type
m < K/scale
where the scale is typical of the highest energy available we tested. At the time of the writing he chose scale = 200 GeV and concluded that m < 1.3 MeV. This has not dramatically improved since.
If somebody has a better reference, I'd be interested.