What Are the Stress and Strain Calculations for Dual Glued Boards Under Load?

[Dell]

in the below question are 2 identical, homogeneous boards, glued together at their centres with the forces applied as in the diagram.

the maximum normal stresses are 30MPa for the boards and 20Mpa for the glue
the maximum shear stresses are 10MPa for the boards and 10Mpa for the glue
the line AB is 10cm long and extends by 0.2mm

1) what are the principal stresses + direction?
2)what are the principal shear stresses + direction?
3)what is the maximum value for P?
4)find E, and V if the maximum xy strain is 2.5e-3?
5)if the boards have a thickness of t, how does the thickness change?

hope the diagram is sufficient

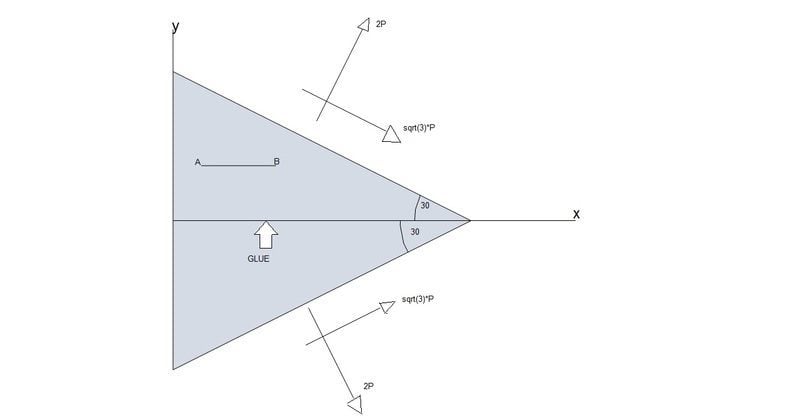
1) what i did was find the forces working on the lefthand side of the triangle
Fxx=2*(2P*cos(60)+sqrt(3)*P*cos(30))
Fxx=5P

Fxy=0

since Fxy is 0, the shear strain σxy is also 0, and therefore the x,y axis would be the principal axis, which is a start.

what i would like to have done here is find the σxx using Fxx/A, but i don't know the area, using parameters

σxx=5P/(L*t) where t is the thickness of the board and L is the side of the equilateral triangle.

now using the transformation equations

σnn=σxx*cos²60)+2*σxy*sin(60)*cos(60)+σyy*sin²(60)
2P/(L*t)=5P/(L*t)*cos²(60) + σyy*sin²(60)
σyy = P/(L*t)(2-5*cos²(60))/sin²(60)
σyy=P/(L*t)

1)principle stress
ϴ=0+90K
σyy=P/(L*t)
σxx=5P/(L*t)

but i still have L and t in my answer.

2) for the principle shear stress

σs=+/- 0.5(5P/(L*t)-P/(L*t))

2)the principle shear stresss'
ϴ=45+90K
σs=+/- 2P/(L*t)
3) i think i need to somehow choose which of the 4 given stresses i need to use to compare to the expressions i found above. since the glue runs parallel to the x-axis I am not sure but i think i need to use the stress state above, in which case the shear stress is 0, and the yy stress in minimal, and the xx stress is irrelevant, so i chose to compare on the board

to find the maximum value of P, i compared the maximum shear strength in the boards to σs that i found

2P/(L*t)=10Mpa
Pmax=5*L*t Mpaand the normal stress
5P/(L*t)=20Mpa
Pmax=4*L*t Mpaof these 2 i chose the smaller one

Pmax=4*L*t Mpa

can someone please check what i have done so far, doesn't seem right to me, for the 1st 2 i would think i need to get rid of the L, t someohow, and for the 3rd i think i need to make more assumptions that that, takeing into account the glue and board, both shearing and normal stress.

thanks

 

[Dell]

what I've tried for 3)- finding V and E

i know that εxy(max)=2.5e-3
and i know that the line AB extended by 0.2mm from its length of 10cm, therefore εxx=2e-3

εxx=(σxx-V*σyy)/E=2e-3
εyy=(σyy-V*σxx)/E
εxy=σxy/(2G)=0/2G=0

εxy(max)=(εxx-εyy)/2 (since εyy and εyy are principle strains (εxy=0) )

lets say P/(L*t)=Q

εxy(max)=\frac{5*Q -VQ+Q-5Q*V}{2E}=\frac{3*Q*(1-V)}{2*E}=2.5e-3

εxx=\frac{5*Q-V*Q}{E}=2e-3

after dividing the 2 i get
V=1.30769
E=1846.153

which can't be since
-1<V<0.5