What are the tension forces in a suspended mass system?

Click For Summary
In a suspended mass system with a gravitational force of 80N, the discussion focuses on determining the tension forces t1, t2, t3, and t4. The user expresses confusion regarding the addition of two more strings and how to approach creating free body diagrams. Assistance is sought for visualizing the forces at the points where the ropes meet. After receiving help, the user acknowledges their improvement but admits that free body diagrams remain a challenge. Understanding the tension forces in such systems is crucial for solving related physics problems effectively.
pbele21
Messages
2
Reaction score
0

Homework Statement


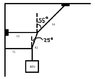
the question is this,
in the figure, find t1,t2, t3, and t4; if Fgrav=80N


Homework Equations





The Attempt at a Solution


the instructor added 2 more stings and I'm really confused where to start on doing free body diagram. hope you guys can help me.. :(
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    7.4 KB · Views: 341
Physics news on Phys.org
Draw free body diagrams for where the ropes meet.
 
thank you for the reply. i got it already. :) my real weakness is doing this free body diagram. thanks again.
 

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?
View full post »

Similar threads

Why are the forces on torque tension and not the weight of the mass?
  • · Replies 7 ·
Replies
7
Views
2K
Conceptual question involving tension and angles
  • · Replies 13 ·
Replies
13
Views
3K
"Tension: T1 vs T2 - What is Correct?
  • · Replies 1 ·
Replies
1
Views
2K
Tension in a deformed cylindrical bag on a surface
  • · Replies 18 ·
Replies
18
Views
2K
What Happens to the Tensions in a Cut String Problem?
  • · Replies 10 ·
Replies
10
Views
3K
Balancing Forces on a Scale: Man with Pulleys and Tensions
  • · Replies 7 ·
Replies
7
Views
2K
Pulleys with Torque: Free Body Diagram Analysis
  • · Replies 34 ·
2
Replies
34
Views
4K
How to find the forces in a particular framework of light rods
  • · Replies 11 ·
Replies
11
Views
2K
Mass and Tension: Comparing Magnitudes
  • · Replies 5 ·
Replies
5
Views
11K
Rocket + Connected Body Dynamics problem
  • · Replies 47 ·
2
Replies
47
Views
3K